题目内容
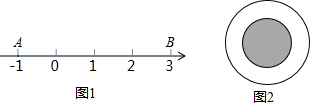
1. 大家知道在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
大家知道在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:(1)数轴上表示x和-2的两点之间的距离表示为|x+2|.
(2)使得等式|x+1|+|x-3|=4成立的x的取值是-1≤x≤3.
(3)当x的取值是1≤x≤2时,式子|x-1|+|x-2|的值最小,最小值是1.
(4)当x的取值是2时,式子|x-1|+|x-2|+|x-3|的值最小,最小值是2…
由此探究:
(5)当x的取值是50时,式子|x-1|+|x-2|+…+|x-99|的值最小,最小值是2450.
(6)当x的取值是50、51时,式子|x-1|+|x-2|+…+|x-100|值最小,最小值是2500.
分析 (1)根据两点之间距离的求法求解即可;
(2)在数轴上表示点到-1和到3的点为4在-1和3之间的点;
(3)使到点1和2距离值最小的点在1和2之间;
(4)有一点到三点的距离和最小的点,是三个数中间的数表示的点;
(5)当有奇数个点,到所有点的距离的最小值是位置处于中间的点;
(6)当有偶数个点,到所有点的距离的最小值是位置处于中间的两个点中的任何一个;由此求得答案即可.
解答 解:(1)数轴上表示x和-2的两点之间的距离表示为|x+2|.
(2)使得等式|x+1|+|x-3|=4成立的x的取值是-1≤x≤3.
(3)当x的取值是1≤x≤2时,式子|x-1|+|x-2|的值最小,最小值是1.
(4)当x的取值是2时,式子|x-1|+|x-2|+|x-3|的值最小,最小值是2…
由此探究:
(5)当x的取值是50时,式子|x-1|+|x-2|+…+|x-99|的值最小,最小值是(1+2+3+4+5+…+49)×2=2450.
(6)当x的取值是50、51时,式子|x-1|+|x-2|+…+|x-100|值最小,最小值是(1+2+3+4+…+49)×2+50=2500.
故答案为:|x+2|;-1≤x≤3;1≤x≤2,1;2,2;50,2450;50、51,2500.
点评 本题考查了数轴,绝对值的性质,理解数轴上两点间的距离的表示和采用数形结合的思想是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.以2和-3为根的方程是( )
| A. | x2+x+6=0 | B. | x2+x-6=0 | C. | x2-x+6=0 | D. | x2-x-6=0 |
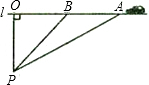 据交管部门统计,超速行驶是引发交通事故的主要原因.某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,双龙大道某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由江宁东山向禄口机场匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
据交管部门统计,超速行驶是引发交通事故的主要原因.某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,双龙大道某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由江宁东山向禄口机场匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)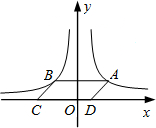 如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$(x<0)的图象于点B,以AB为边作?ABCD,其中C,D在x轴上,则?ABCD的面积为7.
如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$(x<0)的图象于点B,以AB为边作?ABCD,其中C,D在x轴上,则?ABCD的面积为7. 如图:已知梯形ABCD中,AB=AD=CD,BD=BC,求∠A的度数.
如图:已知梯形ABCD中,AB=AD=CD,BD=BC,求∠A的度数.