题目内容
11.计算与化简下面的二次根式(1)2$\sqrt{12}$-$\sqrt{27}$
(2)(3$\sqrt{5}$-1)2
(3)2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷5$\sqrt{2}$
(4)($\sqrt{24}$-$\sqrt{\frac{1}{2}}$)-($\sqrt{\frac{1}{8}}$+$\sqrt{6}$).
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用完全平方公式计算;
(3)根据二次根式的乘除法则运算;
(4)先把各二次根式化为最简二次根式,然后去括号后合并即可.
解答 解:(1)原式=4$\sqrt{3}$-3$\sqrt{3}$
=$\sqrt{3}$;
(2)原式=45-6$\sqrt{5}$+1
=46-6$\sqrt{5}$;
(3)原式=2×$\frac{1}{4}$×$\frac{1}{5}$×$\sqrt{12×\frac{1}{3}×\frac{1}{2}}$
=$\frac{\sqrt{2}}{10}$;
(4)原式=2$\sqrt{6}$-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{4}$-$\sqrt{6}$
=$\sqrt{6}$-$\frac{3\sqrt{2}}{4}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
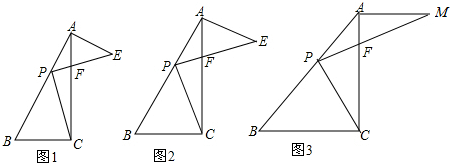
2. 如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )
如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )
 如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )
如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
 已知抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(2,0),与y轴交于点C(0,-2).
已知抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(2,0),与y轴交于点C(0,-2).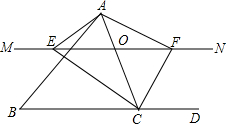 如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. 如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,求菱形ABCD的周长.
如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,求菱形ABCD的周长. 大家知道在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
大家知道在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题: