题目内容
18.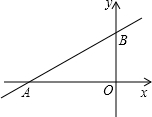 如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2),
如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2),(1)求一次函数解析式;
(2)若点P在一次函数图象上,且△AOP的面积为1,求点P的坐标.
分析 (1)将点A、B坐标代入一次函数y=kx+b求出k、b即可;
(2)设点P的纵坐标为(m,n),根据△AOP的面积为2列出关于n的方程,解方程可得n的值,将n代回解析式可得坐标.
解答 解:(1)设一次函数解析式为:y=kx+b,
根据题意,将点A(-4,0)和点B(0,2)代入得:
$\left\{\begin{array}{l}{-4k+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴一次函数解析式为:y=$\frac{1}{2}$x+2;
(2)设点P的纵坐标为(m,n),
∵OA=4,且△AOP的面积为1,
∴$\frac{1}{2}$×4×|n|=1,
解得:n=$\frac{1}{2}$或n=-$\frac{1}{2}$,
当n=$\frac{1}{2}$时,有$\frac{1}{2}$m+2=$\frac{1}{2}$,解得:m=-3,∴点P(-3,$\frac{1}{2}$);
当n=-$\frac{1}{2}$时,由$\frac{1}{2}$m+2=-$\frac{1}{2}$,解得:m=-5,∴点P(-5,-$\frac{1}{2}$);
综上,点P的坐标为:(-3,$\frac{1}{2}$)或(-5,-$\frac{1}{2}$).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{20}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{7}$ |
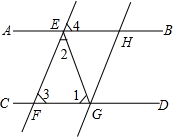 如图所示,下列结论正确的有①③④(把所有正确结论的序号都选上)
如图所示,下列结论正确的有①③④(把所有正确结论的序号都选上)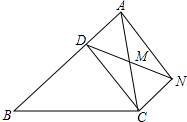 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.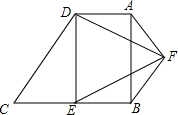 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,E是BC的中点,BC=2AD=$2\sqrt{3}$,△DEF是等边三角形,连结BF、AF.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,E是BC的中点,BC=2AD=$2\sqrt{3}$,△DEF是等边三角形,连结BF、AF.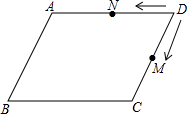 如图,?ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,两点均运动到点D停止.
如图,?ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,两点均运动到点D停止.