题目内容
3.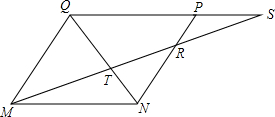 如图,已知MNPQ为平行四边形,在QP的延长线上任取-点S,直线MS与NQ交于点T,与NP交于点R.求证:$\frac{1}{MR}+\frac{1}{MS}=\frac{1}{MT}$.
如图,已知MNPQ为平行四边形,在QP的延长线上任取-点S,直线MS与NQ交于点T,与NP交于点R.求证:$\frac{1}{MR}+\frac{1}{MS}=\frac{1}{MT}$.
分析 由四边形MNPQ平行四边形,得到QM∥PN,推出△SPR∽△SQM,△TRN∽△QMT,于是得到$\frac{SR}{MS}=\frac{PR}{QM}$,$\frac{RT}{MT}=\frac{RN}{QM}$,两式相加得$\frac{SR}{MS}+\frac{RT}{MT}=\frac{PR}{QM}+\frac{RN}{QM}$,通过化简即可得到结论.
解答 解:∵四边形MNPQ平行四边形,
∴QM∥PN,
∴△SPR∽△SQM,△TRN∽△QMT,
∴$\frac{SR}{MS}=\frac{PR}{QM}$,$\frac{RT}{MT}=\frac{RN}{QM}$,
∴$\frac{SR}{MS}+\frac{RT}{MT}=\frac{PR}{QM}+\frac{RN}{QM}$,
∴$\frac{SR}{MS}+\frac{RT}{MT}=1$,
∴$\frac{MS-MR}{MS}$+$\frac{MR-MT}{MT}$=-$\frac{MR}{MS}$+$\frac{MR}{MT}$=1,
∴$\frac{1}{MR}+\frac{1}{MS}=\frac{1}{MT}$.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
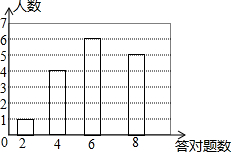 计算机网络知识竞赛,答对1题得10分,某次竞赛结果如图所示(每位参赛选手至少答对2题)
计算机网络知识竞赛,答对1题得10分,某次竞赛结果如图所示(每位参赛选手至少答对2题)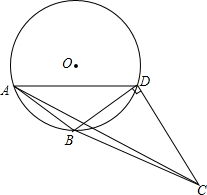 如图,⊙O是△ABD的外接圆,在⊙O外取点C,使得∠BCD=∠BAD,且∠BDC=90°,若∠ADB=30°,求证:BC=2AB.
如图,⊙O是△ABD的外接圆,在⊙O外取点C,使得∠BCD=∠BAD,且∠BDC=90°,若∠ADB=30°,求证:BC=2AB.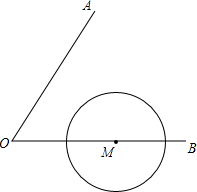 如图,∠AOB=60°,M为OB上的一点,OM=5,若以M为圆心,2.5为半径画⊙M,请通过计算说明OA不和⊙M相切.
如图,∠AOB=60°,M为OB上的一点,OM=5,若以M为圆心,2.5为半径画⊙M,请通过计算说明OA不和⊙M相切. 如图,小明在研究△ABC时,按如下操作“以点A为圆心,以边AB为半径画圆弧,交边AC于点D”得到△BCD,那么BC>CD.(填“>”“<”或“=”)
如图,小明在研究△ABC时,按如下操作“以点A为圆心,以边AB为半径画圆弧,交边AC于点D”得到△BCD,那么BC>CD.(填“>”“<”或“=”)