题目内容
2.已知⊙O中,$\widehat{AB}$=2$\widehat{CD}$,则弦AB和2CD的大小关系是( )| A. | AB>2CD | B. | AB=2CD | C. | AB<2CD | D. | 不能确定 |
分析 如图,取弧AB的中点E,利用$\widehat{AB}$=2$\widehat{CD}$得到$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$,则根据圆心角、弧、弦的关系得到AE=BE=CD,再利用三角形三边的关系得AE+BE>AB,于是有2CD>AB.
解答 解:如图,取弧AB的中点E,则$\widehat{AE}$=$\widehat{BE}$,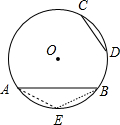 ∵$\widehat{AB}$=2$\widehat{CD}$,
∵$\widehat{AB}$=2$\widehat{CD}$,
∴$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$,
∴AE=BE=CD,
∵AE+BE>AB,
∴2CD>AB.
故选C.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了三角形三边的关系.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
11.如果a<0,b>0,a+b<0,那么下列关系式中正确的是( )
| A. | a>-a>b>-b | B. | b>a>-b>-a | C. | -a>b>-b>a | D. | a>b>-b>-a |
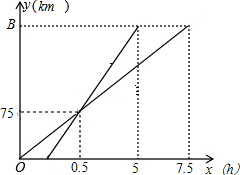 列慢车和一列快车沿相同的路线从A地到B地,所走的路程y(km)与时间x(h)的函数图象如图所示,试根据图象回答下列问题:
列慢车和一列快车沿相同的路线从A地到B地,所走的路程y(km)与时间x(h)的函数图象如图所示,试根据图象回答下列问题: 如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,6)、(-6,5)、(-3,2),试计算△ABC的面积.
如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,6)、(-6,5)、(-3,2),试计算△ABC的面积. 已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.