题目内容
13. 如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,6)、(-6,5)、(-3,2),试计算△ABC的面积.
如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,6)、(-6,5)、(-3,2),试计算△ABC的面积.
分析 作BD⊥x轴,CE⊥x轴,垂足分别为D、E,利用△ABC的面积=梯形ABDO的面积-梯形BDEC的面积-梯形EOAC的面积得出答案即可.
解答 解:如图,
∵点A、B、C的坐标分别为(0,6)、(-6,5)、(-3,2),
∴OA=6,OE=3,CE=2,DE=3,BD=5,
∴S△ABC=S梯形ABDO-S梯形BDEC-S梯形EOAC
=$\frac{1}{2}$×(5+6)×6-$\frac{1}{2}$×(5+2)×3-$\frac{1}{2}$×(2+6)×3
=33-10.5-12
=10.5.
点评 此题考查坐标与图形的性质,利用点的坐标特征,把图形转化为与坐标轴有关的图形的面积解决问题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
8.下列事件中,属于必然事件的是( )
| A. | 在地面向上空跑石块,石块终将落下 | |
| B. | 有一匹马以70米/秒的速度奔跑 | |
| C. | 杭州明年五一节当天的最高气温35℃ | |
| D. | 射击运动员射击一次,命中10环 |
2.已知⊙O中,$\widehat{AB}$=2$\widehat{CD}$,则弦AB和2CD的大小关系是( )
| A. | AB>2CD | B. | AB=2CD | C. | AB<2CD | D. | 不能确定 |
 如图,一张四边形纸片ABCD中,AB∥CD,把它剪一刀,然后拼成一个三角形,要求说明你的剪法和原理,并画出示意图.
如图,一张四边形纸片ABCD中,AB∥CD,把它剪一刀,然后拼成一个三角形,要求说明你的剪法和原理,并画出示意图.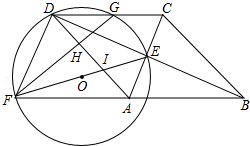 如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.
如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.