题目内容
已知如图，四边形ABCD内接于⊙O，若∠A=60°，则∠DCE=考点：圆内接四边形的性质
专题：
分析：先根据圆内接四边形的对角互补及邻补角互补得出∠A+∠BCD=180°，∠BCD+∠DCE=180°，然后根据同角的补角相等得出∠DCE=∠A=60°．
解答：解：∵四边形ABCD是圆内接四边形，
∴∠A+∠BCD=180°，
∵∠BCD+∠DCE=180°，
∴∠DCE=∠A．
∵∠A=60°，
∴∠DCE=60°．
故答案为：60°．
∴∠A+∠BCD=180°，
∵∠BCD+∠DCE=180°，
∴∠DCE=∠A．
∵∠A=60°，
∴∠DCE=60°．
故答案为：60°．
点评：本题考查的是圆内接四边形的性质，熟知圆内接四边形对角互补的性质是解答此题的关键．
练习册系列答案
相关题目
如图，直线y=kx-2与双曲线y=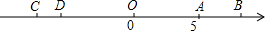
如图，数轴上有两条线段AB和CD，线段AB的长度为4个单位，线段CD的长度为2个单位，点A在数轴上表示的数是5，且A、D两点之间的距离为11．
若⊙O半径为13，圆心在坐标原点上，点P的坐标为（5，12），则点P与⊙O的位置关系是（ ）
| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、不能确定 |