题目内容
若⊙O半径为13，圆心在坐标原点上，点P的坐标为（5，12），则点P与⊙O的位置关系是（ ）
| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、不能确定 |
考点：点与圆的位置关系,坐标与图形性质
专题：
分析：根据P点坐标和勾股定理可计算出OP的长，然后根据点与圆的位置关系的判定方法判断它们的关系．
解答：解：∵圆心P的坐标为（5，12 ），
∴OP=
=13，
∴OP=r，
∴原点O在⊙P上．
故选B．
∴OP=
| 52+122 |
∴OP=r，
∴原点O在⊙P上．
故选B．
点评：本题考查了点与圆的位置关系：设⊙O的半径为r，点P到圆心的距离OP=d，则有：点P在圆外?d＞r；点P在圆上?d=r；点P在圆内?d＜r．
练习册系列答案
相关题目
如图，每个图案均由边长为1的小正方形按一定的规律堆叠而成，照此规律，第10个图案中共有（ ）个小正方形．
| A、50 | B、80 |
| C、100 | D、120 |
已知点（x1，y1）、（x2，y2）在反比例函数y=-
的图象上，如果x1＜x2＜0，则下列结论正确的是（ ）
| 1 |
| x |
| A、y1＜y2 |
| B、y1＞y2 |
| C、y1≤y2 |
| D、y1≥y2 |
已知如图，四边形ABCD内接于⊙O，若∠A=60°，则∠DCE=
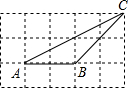如图，在5×3的网格中，每格小正方形的边长都是1，若△ABC的三个顶点都在相应格点上，则sin∠CAB的值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|