题目内容
19.阅读理解:把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数123123,它能(填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M-N的结果能被13整除,这样的四位连接数有几个?
分析 (1)根据六位连接数的定义可知123123为六位连接数,再将123123进行因数分解,判断得出它能被13整除;
(2)设$\overline{abc}$$\overline{abc}$为六位连接数,将$\overline{abc}$$\overline{abc}$进行因数分解,判断得出它能被13整除;
(3)设$\overline{xyxy}$为四位连接数,用含x、y的代数式表示M与N,再计算M-N,然后将$\frac{M-N}{13}$表示为77x+7y+$\frac{3x+4y}{13}$,根据M-N的结果能被13整除以及M与N都是1~9之间的整数,求得x与y的值,即可求解.
解答 解:(1)123123为六位连接数;
∵123123=123×1001=123×13×77,
∴123123能被13整除;
(2)任意六位连接数都能被13整除,理由如下:
设$\overline{abc}$$\overline{abc}$为六位连接数,
∵$\overline{abc}$$\overline{abc}$=$\overline{abc}$×1001=$\overline{abc}$×13×77,
∴$\overline{abc}$$\overline{abc}$能被13整除;
(3)设$\overline{xyxy}$为四位连接数,
则M=1000x+100y+10x+y=1010x+101y,N=3(x+y+x+y)=6x+6y,
∴M-N=(1010x+101y)-(6x+6y)=1004x+95y,
∴$\frac{M-N}{13}$=$\frac{1004x+95y}{13}$=77x+7y+$\frac{3x+4y}{13}$,
∵M-N的结果能被13整除,
∴$\frac{3x+4y}{13}$是整数,
∵M与N都是1~9之间的整数,
∴x=1,y=9;x=2,y=5;x=3,y=1;
∴这样的四位连接数有1919,2525,3131,一共3个.
点评 本题考查了因式分解的应用,整式的运算,理解“连接数”的定义是解题的关键.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | 6,8,10 | B. | 4,5,7 | C. | 2,3,4 | D. | 1,2,3 |
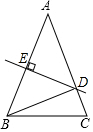 如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.