题目内容
7.有下面的等式:①$\sqrt{2}+\sqrt{8}=\sqrt{18}$②$\sqrt{{{(-2)}^2}}=2$③$\sqrt{2}•\sqrt{8}=4$④$\frac{2}{{\sqrt{2}}}=\sqrt{2}$,其中成立的有( )| A. | ①②③④ | B. | ②③④ | C. | ②③ | D. | ①③ |
分析 根据二次根式混合运算的方法,逐项判定即可.
解答 解:∵$\sqrt{2}$+$\sqrt{8}$=3$\sqrt{2}$,
∴选项①不符合题意;
∵$\sqrt{{{(-2)}^2}}=2$,
∴选项②符合题意;
∵$\sqrt{2}•\sqrt{8}=4$,
∴选项③符合题意;
∵$\frac{2}{{\sqrt{2}}}=\sqrt{2}$,
∴选项④符合题意,
∴成立的有3个:②③④.
故选:B.
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.

练习册系列答案
相关题目
18.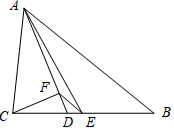 如图,△ABC中,AB=4,AC=2,AD、AE分别是其角平分线和中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为( )
如图,△ABC中,AB=4,AC=2,AD、AE分别是其角平分线和中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为( )
 如图,△ABC中,AB=4,AC=2,AD、AE分别是其角平分线和中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为( )
如图,△ABC中,AB=4,AC=2,AD、AE分别是其角平分线和中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
12.如果关于x的不等式(m-1)x<m-1的解集为x>1,那么m的取值范围是( )
| A. | m≠1 | B. | m<0 | C. | m>1 | D. | m<1 |
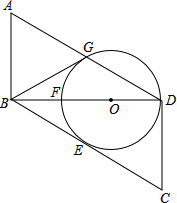 如图,在?ABCD中,对角线BD⊥CD,O为对角线BD上一点,以O为圆心的圆与BC相切于点E,交BD于点F,交AD于点G.
如图,在?ABCD中,对角线BD⊥CD,O为对角线BD上一点,以O为圆心的圆与BC相切于点E,交BD于点F,交AD于点G. 如图2,AB∥CD,BE⊥DE,∠ABE=155°37′,求∠CDE的大小.
如图2,AB∥CD,BE⊥DE,∠ABE=155°37′,求∠CDE的大小.