题目内容
2. 如图,△ABC是等边三角形,△ABP旋转后能与△CBP′重合.
如图,△ABC是等边三角形,△ABP旋转后能与△CBP′重合.(1)旋转中心是哪一点?
(2)旋转角度是多少度?
(3)连结PP′后,△BPP′是什么三角形?简单说明理由.
分析 (1)根据旋转后点B的没有改变可知点B就是旋转中心;
(2)找出旋转前后AB与BC是对应边,所以AB与BC的夹角等于旋转角度的度数,再根据等边三角形的内角都是60°进行求解;
(3)利用旋转的性质结合等边三角形的判定方法得出答案.
解答 解:(1)∵△ABP旋转后能与△P'BC重合,点B是对应点,没有改变,
∴点B是旋转中心;
(2)AB与BC是旋转前后对应边,
旋转角=∠ABC,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴旋转角是60°;
(3)连结PP′后,△BPP′是等边三角形,
理由:∵旋转角是60°,
∴∠PBP′=60°,
又∵BP=BP′,
∴△BPP′是等边三角形.
点评 本题考查了旋转的性质,旋转中心的确定,旋转角的确定,等边三角形的判定等知识,正确掌握旋转的性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列算式正确的( )
| A. | $\frac{(-a+b)^{2}}{(a-b)^{2}}$=1 | B. | $\frac{-a-1}{-a^2+8}$=$\frac{a-1}{a^2+8}$ | ||
| C. | $\frac{x^2+y^2}{x+y}$=x+y | D. | $\frac{0.5+2y}{0.1+x}$=$\frac{5+2y}{1+x}$ |
14.下列说法正确的是( )
| A. | 周长相等的锐角三角形都全等 | B. | 周长相等的直角三角形都全等 | ||
| C. | 周长相等的钝角三角形都全等 | D. | 周长相等的等边三角形都全等 |
11.现有两辆汽车从相距120km的A,B两地同时出发匀速行驶,如果两辆车的行驶方向相同,那么6h后,速度快的汽车追上速度慢的汽车,如果两辆车相向行驶,那么1.2h后两车相遇,则速度快的汽车和速度慢的汽车的速度分别为( )
| A. | 60km/h和40km/h | B. | 80km/h和60km/h | C. | 40km/h和20km/h | D. | 80km/h和40km/h |
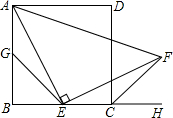 如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.
如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG. 如图所示的正方形网格中,每小格均为边长是1的正方形,△ABC的三个顶点的坐标分别为A(0,2)、B(1,0)、C(3,4).请在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,每小格均为边长是1的正方形,△ABC的三个顶点的坐标分别为A(0,2)、B(1,0)、C(3,4).请在所给直角坐标系中解答下列问题: 如图所示,在边长为1的网格中,请按要求画出图形.
如图所示,在边长为1的网格中,请按要求画出图形. 如图,直线y=-2x+2与x轴,y轴分别相交于点A、B,四边形ABCD是正方形,双曲线y=$\frac{k}{x}$在第一象限经过点D,将正方形向下平移m个单位后,点C刚好落在双曲线上,则m=$\frac{3}{2}$.
如图,直线y=-2x+2与x轴,y轴分别相交于点A、B,四边形ABCD是正方形,双曲线y=$\frac{k}{x}$在第一象限经过点D,将正方形向下平移m个单位后,点C刚好落在双曲线上,则m=$\frac{3}{2}$.