题目内容
13.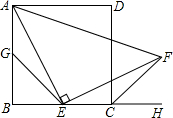 如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.
如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.(1)猜想:△AGE与△ECF全等吗?线段EG和CF的长度相等吗?
(2)将△ECF绕点E逆时针旋转90°,请在图中直接画出旋转后的图形,并指出旋转后CF与EG的位置关系.
分析 (1)G、E分别为AB、BC的中点,由正方形的性质可知AG=EC,△BEG为等腰直角三角形,则∠AGE=180°-45°=135°,而∠ECF=90°+45°=135°,得∠AGE=∠ECF,再利用互余关系,得∠GAE=90°-∠AEB=∠CEF,根据ASA可证△AGE≌△ECF;
(2)先将△ECF绕点E逆时针旋转90°后得△EMA,再根据旋转的性质以及全等三角形的性质,可得∠MAE=∠GEA,进而得出旋转后CF与EG互相平行.
解答 解:(1)△AGE与△ECF全等,线段EG和CF的长度相等.
∵正方形ABCD中,点G,E为边AB、BC中点,
∴AG=EC,△BEG为等腰直角三角形,
∴∠AGE=180°-45°=135°,
又∵CF为正方形外角平分线,
∴∠ECF=90°+45°=135°,
∵∠AEF=90°,
∴∠GAE=90°-∠AEB=∠CEF,
∵在△AGE和△ECF中,
$\left\{\begin{array}{l}{∠AGE=∠ECF}\\{AG=CE}\\{∠GAE=∠CEF}\end{array}\right.$,
∴△AGE≌△ECF(ASA),
∴EG=FC;
(2)如图,将△ECF绕点E逆时针旋转90°后可得△EMA,
由旋转得,∠CFE=∠MAE,
由△AGE≌△ECF可得,∠CFE=∠GEA,
∴∠MAE=∠GEA,
∴AM∥GE,即旋转后CF与EG互相平行.
点评 本题主要考查了全等三角形的判定以及旋转的性质,解决问题的关键是掌握:两角及其夹边分别对应相等的两个三角形全等,旋转前、后的图形全等.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
5.下面生活中,物体的运动情况可以看成平移的是( )
| A. | 时钟摆动的钟摆 | B. | 在笔直的公路上行驶的汽车 | ||
| C. | 随风摆动的旗帜 | D. | 汽车玻璃窗上两刷的运动 |
3.在平面直角坐标系中,若将点A(3,-2)向左平移5个单位长度得到点A1,则点A1的坐标为( )
| A. | (3,-7) | B. | (3,3) | C. | (8,-2) | D. | (-2,-2) |

 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标 是(-3,-1).将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标.
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标 是(-3,-1).将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标. 如图,在平面直角坐标系xOy中,点A(0,m+4),点C(5m+3,0)在x轴的正半轴上,现将点C向左平移4单位长度再向上平移7个单位长度得到对应点B(7m-7,n).
如图,在平面直角坐标系xOy中,点A(0,m+4),点C(5m+3,0)在x轴的正半轴上,现将点C向左平移4单位长度再向上平移7个单位长度得到对应点B(7m-7,n).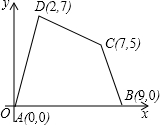 如图,已知四边形ABCD四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7).将该四边形先向右平移2个单位,再向下平移3个单位后得到四边形A1B1C1D1,求四边形A1B1C1D1的面积.
如图,已知四边形ABCD四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7).将该四边形先向右平移2个单位,再向下平移3个单位后得到四边形A1B1C1D1,求四边形A1B1C1D1的面积. 如图,△ABC是等边三角形,△ABP旋转后能与△CBP′重合.
如图,△ABC是等边三角形,△ABP旋转后能与△CBP′重合.