题目内容
3.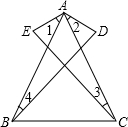 如图,∠3=∠4,AE=AD,∠1=∠2.求证:AC=AB.
如图,∠3=∠4,AE=AD,∠1=∠2.求证:AC=AB.
分析 求出∠BAD=∠CAE,再利用“角角边”证明△ABD和△ACE全等,根据全等三角形对应边相等证明即可.
解答 证明:∵∠1=∠2,
∴∠1+∠BAC=∠2+∠BAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,$\left\{\begin{array}{l}{∠BAD=∠CAE}\\{∠3=∠4}\\{AE=AD}\end{array}\right.$,
∴△ABD≌△ACE(AAS),
∴AC=AB.
点评 本题考查了全等三角形的判定与性质,熟练掌握三角形全等的判定方法是解题的关键,难点在于求出∠BAD=∠CAE.

练习册系列答案
相关题目
11.若|a-2|+b2+4b+4+$\sqrt{{c}^{2}-c+\frac{1}{4}}$=0,则$\sqrt{{b}^{2}}$•$\sqrt{a}$•$\sqrt{c}$的值是( )
| A. | 4 | B. | 2 | C. | -2 | D. | 1 |
18.甲、乙两班学生到集市上购买苹果,苹果的价格如表:
甲班分两次购买60千克(第二次多于第一次),而乙班一次购买苹果60千克.
(1)若甲班第一次购买28千克,第二次购买32千克,则乙班比甲班少付多少元?
(2)若甲班两次共付费163元,则甲班第一次、第二次分别购买苹果多少千克?
| 所购苹果数量 | 不超过30千克 | 30千克以上但不超过50千克 | 50千克以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
(1)若甲班第一次购买28千克,第二次购买32千克,则乙班比甲班少付多少元?
(2)若甲班两次共付费163元,则甲班第一次、第二次分别购买苹果多少千克?
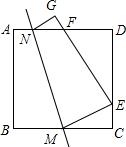 如图,将正方形ABCD沿直线MN折叠,使B点落在CD边上,AB边折叠后与AD边交于F,若三角形DEF与三角形ECM的周长差为3,则DE的长为3.
如图,将正方形ABCD沿直线MN折叠,使B点落在CD边上,AB边折叠后与AD边交于F,若三角形DEF与三角形ECM的周长差为3,则DE的长为3.
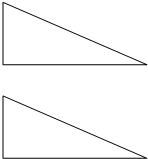 将两个全等的直角三角形,拼成一个四边形.那么这些图形中有4个轴对称图形.
将两个全等的直角三角形,拼成一个四边形.那么这些图形中有4个轴对称图形.