题目内容
8.请确定下列函数的开口方向、对称轴及顶点坐标、最大值或最小值,并研究其增减性.(1)y=x2+x-2(-1<x<2)
∴抛物线开口方向上,对称轴x=-$\frac{1}{2}$,顶点坐标(-$\frac{1}{2}$,$\frac{9}{4}$),当x=-$\frac{1}{2}$时,函数有最值是-$\frac{9}{4}$,在对称轴的左侧y随x的增大而减小,在对称轴的右侧y随x的增大而增大.
(2)y=$\frac{1}{2}{x}^{2}$-4x+8
∴抛物线开口方向上,对称轴x=4,顶点坐标(4,0),当x=4时,函数有最值是0,在对称轴的左侧y随x的增大而减小,在对称轴的右侧y随x的增大而增大.
分析 把二次函数解析式化为顶点式,可求得开口方向、对称轴和顶点坐标,再结合函数的增减性可分别得出答案.
解答 解:
(1)∵y=x2+x-2=(x+$\frac{1}{2}$)2-$\frac{9}{4}$,
∴抛物线开口方向上,对称轴x=-$\frac{1}{2}$,顶点坐标为(-$\frac{1}{2}$,-$\frac{9}{4}$),
∵-1<x<2,
∴当x=-$\frac{1}{2}$时,函数有最值是-$\frac{9}{4}$,
∵抛物线开口方向上,对称轴x=-$\frac{1}{2}$,
∴在对称轴的左侧y随x的增大而减小,在对称轴的右侧y随x的增大而增大,
故答案为:上;x=-$\frac{1}{2}$;(-$\frac{1}{2}$,-$\frac{9}{4}$);-$\frac{1}{2}$;-$\frac{9}{4}$;减小;增大;
(2)∵y=$\frac{1}{2}{x}^{2}$-4x+8=$\frac{1}{2}$(x-4)2,
∴抛物线开口方向上,对称轴x=4,顶点坐标为(4,0),
∵当x<4时,y随x的增大而增大,
∴当x=2时函数有最小值是2,
∵抛物线开口方向上,对称轴x=4,
∴在对称轴的左侧y随x的增大而减小,在对称轴的右侧y随x的增大而增大,
故答案为:上;x=4;(4,0);2;2;减小;增大;
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,顶点坐标为(h,k),对称轴为x=h.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列计算正确的是( )
| A. | $\sqrt{2}$$•\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{2}•\sqrt{3}=\sqrt{6}$ | C. | $\sqrt{8}$=4 | D. | $\sqrt{(-3)^{2}}$=-3 |
18.如果|y+3|+(2x-4)2=0,那么2x-y的值为( )
| A. | 1 | B. | -1 | C. | -7 | D. | 7 |
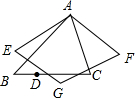 如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,D点关于AB,AC的对称点分别是E和F,四边形AEGF是平行四边形,则四边形AEGF的面积的最小值是$\sqrt{3}$.
如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,D点关于AB,AC的对称点分别是E和F,四边形AEGF是平行四边形,则四边形AEGF的面积的最小值是$\sqrt{3}$.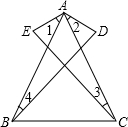 如图,∠3=∠4,AE=AD,∠1=∠2.求证:AC=AB.
如图,∠3=∠4,AE=AD,∠1=∠2.求证:AC=AB. 如图,在△ABC中,AB=AC=10,sinB=$\frac{3}{5}$,
如图,在△ABC中,AB=AC=10,sinB=$\frac{3}{5}$,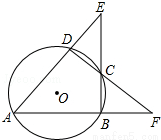 如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.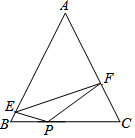 已知:如图,在△ABC中,AB=AC且tanA=$\frac{4}{3}$,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=2$\sqrt{13}$.
已知:如图,在△ABC中,AB=AC且tanA=$\frac{4}{3}$,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=2$\sqrt{13}$.