题目内容
19.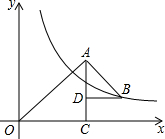 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{6}{x}$在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC-S△BAD为( )
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{6}{x}$在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC-S△BAD为( )| A. | 3 | B. | 6 | C. | 12 | D. | 36 |
分析 设△OAC和△BAD的直角边长分别为a、b,结合等腰直角三角形的性质及图象可得出点B的坐标,根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论.
解答 解:设△OAC和△BAD的直角边长分别为a、b,则点B的坐标为(a+b,a-b).
∵点B在反比例函数y=$\frac{6}{x}$的第一象限图象上,
∴(a+b)×(a-b)=a2-b2=6.
∴S△OAC-S△BAD=$\frac{1}{2}$a2-$\frac{1}{2}$b2=$\frac{1}{2}$(a2-b2)=$\frac{1}{2}$×6=3.
故选:A.
点评 本题考查了反比例函数系数k的几何意义、等腰三角形的性质以及三角形面积公式的运用,解题的关键是设等腰直角三角形的直角边分别为a、b,用其表示出反比例函数上点的坐标.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
9.在数轴上,与2所在的点距离是2个单位长度的点所表示的数是( )
| A. | 0 | B. | 4 | C. | 2和-2 | D. | 0和4 |
10. 我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:
我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:
(1)把上表中x、y的各组对应值作为点的坐标,在给出的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式及自变量x的取值范围;
(2)若市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
 我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:
我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)若市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
14.某人下午6点到7点之间外出购物,出发和回来时发现表上的时针和分针的夹角都为110°,此人外出购物共用了( )分钟.
| A. | 16 | B. | 20 | C. | 32 | D. | 40 |
4.下列说法中不正确的是( )
| A. | 经过有交通信号灯的路口,遇到红灯是随机事件 | |
| B. | 某妇产医院里,下一个出生的婴儿是女孩是必然事件 | |
| C. | 357人中至少有2人生日(公历)相同是确定事件 | |
| D. | 长分别为3,5,9厘米的三条线段不能围成一个三角形是确定事件 |
10. 如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )
如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )
 如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )
如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )| A. | 80° | B. | 45° | C. | 60° | D. | 70° |
 如图,△ABC中,AC=13,AB=12,BC=5,CD是△ABC的角平分线,DE⊥AC于E,连结EB.
如图,△ABC中,AC=13,AB=12,BC=5,CD是△ABC的角平分线,DE⊥AC于E,连结EB.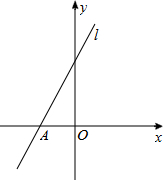 如右图,在直角坐标系中,点A(-4,0),直线l与x轴夹角为60°,点B在直线l上,且AB=10,求点B的坐标.
如右图,在直角坐标系中,点A(-4,0),直线l与x轴夹角为60°,点B在直线l上,且AB=10,求点B的坐标.