题目内容
4.在Rt△OAB中,∠OAB=15°,OC为斜边上的高,且OC=1,P,Q分别为△AOC和△BOC的内心(内心为三角形三条角平分线的交点),连接PQ并延长交OB于M,则OM=( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 根据内心的概念证明△POC∽△QBC,根据相似三角形的性质得到$\frac{PC}{CQ}$=$\frac{OB}{OA}$,证明△PCQ∽△AOB,得到∠CPQ=∠A=15°,证明△COQ≌△MOQ即可.
解答 解:∵∠AOB=90°,∠ACO=90°,
∴∠AOC=∠ABO,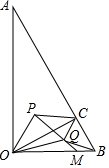 ∵P,Q分别为△AOC和△BOC的内心,
∵P,Q分别为△AOC和△BOC的内心,
∴∠POC=∠QBC,∠PCO=∠BCQ=45°,
∴△POC∽△QBC,
∴$\frac{PC}{CQ}$=$\frac{OC}{BC}$,
∵$\frac{OB}{OA}$=$\frac{OC}{BC}$,
∴$\frac{PC}{CQ}$=$\frac{OB}{OA}$,又∠AOB=∠PCQ=90°,
∴△PCQ∽△AOB,
∴∠CPQ=∠A=15°,
由内心的概念可知,∠OPC=90°+$\frac{1}{2}$×15°,
∴∠OPM=90°+$\frac{1}{2}$×15°-15°,
∵∠POM=90°-$\frac{1}{2}$∠AOC=90°-$\frac{1}{2}$×75°,
∴∠PMO=45°,
在△COQ和△MOQ中,
$\left\{\begin{array}{l}{∠COQ=∠MOQ}\\{∠OCQ=∠OMQ}\\{OQ=OQ}\end{array}\right.$,
∴△COQ≌△MOQ,
∴OM=OC=1,
故选:B.
点评 本题考查的是三角形的内接圆和内心的概念、相似三角形的判定和性质、全等三角形的判定和性质,掌握三角形的内接圆和内心的概念是解题的关键.

练习册系列答案
相关题目
12.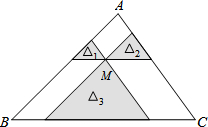 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )
 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )| A. | 62 | B. | 186 | C. | 132 | D. | 144 |
19.能说明命题“对于任何实数a,a2≥a”是假命题的一个反例可以是( )
| A. | a=-2 | B. | a=1 | C. | a=0 | D. | a=0.2 |
9.在数轴上,与2所在的点距离是2个单位长度的点所表示的数是( )
| A. | 0 | B. | 4 | C. | 2和-2 | D. | 0和4 |
16.4的算术平方根是( )
| A. | y=2x-1 | B. | 2 | C. | 4 | D. | ±2 |
14.某人下午6点到7点之间外出购物,出发和回来时发现表上的时针和分针的夹角都为110°,此人外出购物共用了( )分钟.
| A. | 16 | B. | 20 | C. | 32 | D. | 40 |
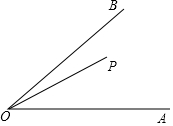 如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$.
如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$. 油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片102片或者长方形铁片80片,如图,一个油桶由两个圆形铁片和一个长方形铁片相配套,生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?
油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片102片或者长方形铁片80片,如图,一个油桶由两个圆形铁片和一个长方形铁片相配套,生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?