题目内容
7. 如图,已知等边△ABC,D、E分别在 BC、AC上,且BD=CE,连接BE、AD交于F点.求证:∠AFE=60°.
如图,已知等边△ABC,D、E分别在 BC、AC上,且BD=CE,连接BE、AD交于F点.求证:∠AFE=60°.
分析 因为△ABC为等边三角形,所以∠ABD=∠BCE=60°,AB=AC=BC,又BD=CE,所以用“SAS”可判定△ABD≌△BCE,根据全等三角形的性质得出∠BAD=∠CBE,利用三角形外角性质解答即可;
解答 解:∵△ABC为等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°,
在△ABD和△BCE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠BCE=60°}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△BCE(SAS);
∴∠BAD=∠CBE,
∵∠ADC=∠CBE+∠BFD=∠BAD+∠B,
∴∠BFD=∠B=∠AFE=60°.
点评 本题考查了全等三角形的判定和性质,关键是根据等边三角形的性质:等边三角形的三个内角都相等,且都等于60°;三条边相等.

练习册系列答案
相关题目
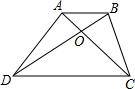 如图,在梯形ABCD中,AB∥DC,AB=a,CD=b(a<b),若△BOC的面积为梯形面积的$\frac{2}{9}$,则$\frac{a}{b}$=$\frac{1}{2}$.
如图,在梯形ABCD中,AB∥DC,AB=a,CD=b(a<b),若△BOC的面积为梯形面积的$\frac{2}{9}$,则$\frac{a}{b}$=$\frac{1}{2}$. 如图,已知Rt△ABC,∠ACB=90°,AD平分∠BAC与BC交于D点,M、N分别在线段AD、AC上的动点,连接MN、MC,当MN+MC最小时,画出M、N的位置.已知△ABC的面积为12cm2,AB=6cm,求MN+MC的最小值.
如图,已知Rt△ABC,∠ACB=90°,AD平分∠BAC与BC交于D点,M、N分别在线段AD、AC上的动点,连接MN、MC,当MN+MC最小时,画出M、N的位置.已知△ABC的面积为12cm2,AB=6cm,求MN+MC的最小值.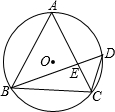 如图,等边三角形ABC内接于⊙O,D为$\widehat{AC}$上一点,连接BD交AC于点E,若∠ABD=45°,则∠AED=105度.
如图,等边三角形ABC内接于⊙O,D为$\widehat{AC}$上一点,连接BD交AC于点E,若∠ABD=45°,则∠AED=105度.