题目内容
17.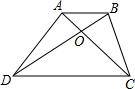 如图,在梯形ABCD中,AB∥DC,AB=a,CD=b(a<b),若△BOC的面积为梯形面积的$\frac{2}{9}$,则$\frac{a}{b}$=$\frac{1}{2}$.
如图,在梯形ABCD中,AB∥DC,AB=a,CD=b(a<b),若△BOC的面积为梯形面积的$\frac{2}{9}$,则$\frac{a}{b}$=$\frac{1}{2}$.
分析 由于AB∥DC,可得出△OAB∽△ODC;根据OA、OD的长,已知两个三角形的相似比;由相似三角形的面积比等于相似比的平方,即可求出$\frac{a}{b}$的值.
解答 解:由题意知:△AOB∽△DOC,则OA:OC=AB:CD=OB:OD=a:b,
∴$\frac{{S}_{△BOC}}{{S}_{△ABO}}$=$\frac{OC}{OA}$=$\frac{b}{a}$,
∴$\frac{{S}_{△BOC}}{{S}_{△ABC}}$=$\frac{b}{a+b}$,
又∵$\frac{{S}_{△ABC}}{{S}_{ADC}}$=$\frac{AB}{CD}$=$\frac{a}{b}$,
∴$\frac{{S}_{△ABC}}{{S}_{梯形ABCD}}$=$\frac{a}{a+b}$,
即$\frac{{S}_{△BOC}}{{S}_{梯形ABCD}}$=$\frac{b}{a+b}$•$\frac{a}{a+b}$=$\frac{2}{9}$.
∴2(a+b)2=9ab,
整理得:(2a-b)(a-2b)=0,
∵a<b,
∴2a=b,即$\frac{a}{b}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题主要考查了相似三角形的判定与性质,熟知相似三角形的面积比等于相似比的平方是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
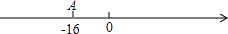 已知A、B两地相距50米,小乌龟从A地出发前往B地,第一次它前进1米,第二次它后退2米,第三次再前进3米,第四次又向后退4米…,按此规律行进,如果A地在数轴上表示的数为-16.
已知A、B两地相距50米,小乌龟从A地出发前往B地,第一次它前进1米,第二次它后退2米,第三次再前进3米,第四次又向后退4米…,按此规律行进,如果A地在数轴上表示的数为-16.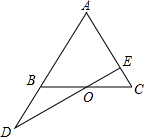 如图,已知点O是△ABC中BC边上的中点,且$\frac{BD}{AB}$=$\frac{3}{5}$,则$\frac{CE}{AE}$=$\frac{3}{8}$.
如图,已知点O是△ABC中BC边上的中点,且$\frac{BD}{AB}$=$\frac{3}{5}$,则$\frac{CE}{AE}$=$\frac{3}{8}$. 如图,已知等边△ABC,D、E分别在 BC、AC上,且BD=CE,连接BE、AD交于F点.求证:∠AFE=60°.
如图,已知等边△ABC,D、E分别在 BC、AC上,且BD=CE,连接BE、AD交于F点.求证:∠AFE=60°.