��Ŀ����
1����ƽ��ֱ������ϵxOy�У���֪��A������Ϊ��0��-1������C��m��0����x���ϵ�һ�����㣮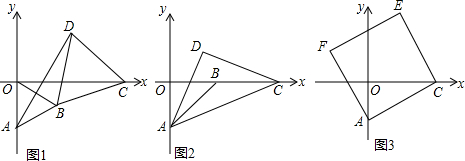
��1����ͼ1����AOB�͡�BCD���ǵȱ������Σ�����C��x�����˶�����ͼ��ʾλ��ʱ������AD����֤����ABD�ա�OBC��
��2����ͼ2����ABO�͡�ACD���ǵ���ֱ�������Σ�����C��x�����˶���m��1��ʱ�����D������Ϊ��x��y������̽��y��x֮��ĺ�����ϵʽ��
��3����ͼ3���ı���ACEF�������Σ�����C��x�����˶���m��1��ʱ�����E������Ϊ��x��y������̽��y��x֮��ĺ�����ϵʽ��
���� ��1���ɵȱ������ε����ʵõ�AB=OB��BD=BC����ABO=��DBC=60�㣬�Ӷ��жϳ���ABD=��OBC���ɣ�
��2�����ɡ�ABO�͡�ACD���ǵ���ֱ�������Σ��ó�$\frac{AO}{AB}=\frac{AD}{AC}$���Ӷ��õ����������ƣ����ɣ�
��3����DG��EH���õ�$\frac{AD}{AE}=\frac{AG}{AH}$=$\frac{DG}{EF}$�������������ε����ʼ��ɣ�
��� �⣺��1���ߡ�AOB�͡�BCD���ǵȱ������Σ�
��AB=OB��BD=BC����ABO=��DBC=60�㣬
���ABD=��OBC��
�ڡ�ABD�͡�OBC�У�
$\left\{\begin{array}{l}{AB=OB}\\{��ABD=��OBC}\\{BD=BC}\end{array}\right.$��
���ABD�͡�OBC��
��2���ߡ�ABO�͡�ACD���ǵ���ֱ�������Σ�
��$\frac{AO}{AB}=\frac{AD}{AC}$��
�ߡ�OAD=��BAC��
���AOD�ס�ABC��
���AOD=��ABC=135��Ϊ��ֵ��
��y��x֮��Ĺ�ϵ��y=x��
��3����ͼ��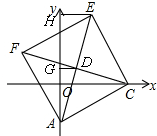
����AE��CF���ڵ�D����D��a��a��������D��DG��y�ᣬ����E��EH��y����H��
��DG��EH��
��$\frac{AD}{AE}=\frac{AG}{AH}$=$\frac{DG}{EF}$��
�ߵ�D��������ACEF�ĶԽ��߽��㣬
��AD=ED=$\frac{1}{2}$AE��
��AG=a+1��AH=2a+2��DG=a��EH=2a��
��OH=2a+1��
��y=2a+1��x=2a��
��y=x+1��
���� �������ı����ۺ��⣬��Ҫ�����˵ȱ������Σ�����ֱ�������ε����ʣ������ε����ƺ�ȫ�ȵ����ʺ��ж����Ȿ��Ĺؼ����ж����������ƣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | -2 | B�� | 3 | C�� | 0 | D�� | $\sqrt{6}$ |
 ��ͼ��ij��ɽ�˶�Ա��Ӫ��A���½�Ϊ30���б��AB����ɽ��B�����AB=600m����ô��ʵ�������ĸ߶�BCΪ��������
��ͼ��ij��ɽ�˶�Ա��Ӫ��A���½�Ϊ30���б��AB����ɽ��B�����AB=600m����ô��ʵ�������ĸ߶�BCΪ��������| A�� | 300$\sqrt{3}$m | B�� | 1200m | C�� | 300m | D�� | 200$\sqrt{3}$m |
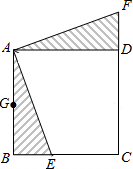 ��ͼ����������ABCD�У�E��BC��һ�㣬��ABE������ת��õ���ADF��
��ͼ����������ABCD�У�E��BC��һ�㣬��ABE������ת��õ���ADF��

 ��ͼ��˫����y=$\frac{k}{x}$��ֱ��y=x-2�ཻ��A��B���㣬��A��������Ϊ1��
��ͼ��˫����y=$\frac{k}{x}$��ֱ��y=x-2�ཻ��A��B���㣬��A��������Ϊ1��