题目内容
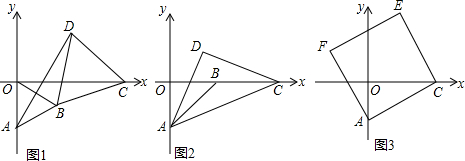
17.操作与实践(1)如图1,已知△ABC,过点A画一条平分三角形面积的直线;(简述作图过程)
(2)如图2,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO的面积相等;
(3)如图3,点M在△ABC的边上,过点M画一条平分三角形面积的直线.(简述作图过程)
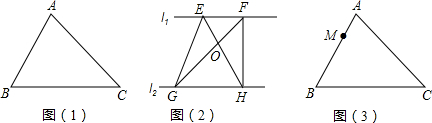
分析 (1)作三角形ABC的中线AD,根据三角形面积公式可判断直线AD平分△ABC的面积;
(2)利用两平行线的距离对应可判断点E和点F到GH的距离相等,根据三角形面积公式可判断S△EGH=S△FGH,然后都减去△OGH的面积即可得到△EGO与△FHO的面积相等;
(3)先作中线AD,连结MD,然后过A点作MD的平行线交BC于N,则利用(1)、(2)的结论可判断MN平分△ABC的面积.
解答 解:(1)如图(1),中线AD所在的直线为所作;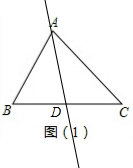
因为点为AD的中点,
所以AD=CD,
所以S△ABD=S△ACD;
(2)如图(2),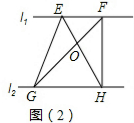
∵l1∥l2,
∴S△EGH=S△FGH,
即S△EGO+S△OGH=S△FOH+S△OGH,
∴S△EGO=S△FOH;
(3)如图3,MN为所作.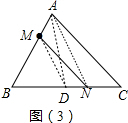
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了三角形面积公式.

练习册系列答案
相关题目
8.下列计算错误的是( )
| A. | x•x5=x6 | B. | a6÷a2=a3 | C. | (ab2)3=a3b6 | D. | (-a2)2=a4 |
5.已知-4a5bm÷28anb2=-$\frac{1}{7}$b2,则m、n的值为( )
| A. | m=4,n=2 | B. | m=4,n=5 | C. | m=1,n=3 | D. | m=2,n=3 |
8.一组数据1,2,3,4,5的方差为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
5.下列命题正确的是( )
| A. | 一组对边相等,另一组对边平行的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
6.不等式2x-2≤0的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
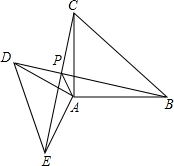 如图,在△ABC和△ADE中,∠CAB=∠DAE=90°,AB=AC=4,AD=AE=2,直线,CE交BD于点P,将△ADE绕点A旋转α角(0°<α<180°),在旋转过程中,S△PAB的最大值为2+2$\sqrt{3}$.
如图,在△ABC和△ADE中,∠CAB=∠DAE=90°,AB=AC=4,AD=AE=2,直线,CE交BD于点P,将△ADE绕点A旋转α角(0°<α<180°),在旋转过程中,S△PAB的最大值为2+2$\sqrt{3}$.