题目内容
12.已知x2+4x+1=0,求(x-1)2+($\frac{1}{x}$-1)2=24.分析 根据完全平方公式,即可解答.
解答 解:∵x2+4x+1=0,
∴x+4+$\frac{1}{x}$=0,
∴x+$\frac{1}{x}$=-4,
$(x-1)^{2}+(\frac{1}{x}-)^{2}$
=x2-2x+1+$\frac{1}{{x}^{2}}-\frac{2}{x}$+1
=$(x+\frac{1}{x})^{2}-2(x+\frac{1}{x})$
=16-2×(-4)
=24.
故答案为:24.
点评 本题考查了完全平方公式,解决本题的关键是熟记完全平方公式的定义.

练习册系列答案
相关题目
20.(-0.7)2的平方根是( )
| A. | -0.7 | B. | 0.7 | C. | ±0.7 | D. | 0.49 |
17. 在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )
在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )
 在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )
在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )| A. | 1+$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | 2$\sqrt{2}$+1 |
1.下列各式不能用平方差公式法分解因式的是( )
| A. | x2-4 | B. | -x2-y2+2xy | C. | m2n2-1 | D. | a2-4b2 |
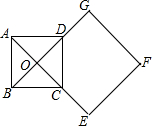 如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG=$\sqrt{2}$AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=30或150度时,∠OAG′=90°.
如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG=$\sqrt{2}$AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=30或150度时,∠OAG′=90°.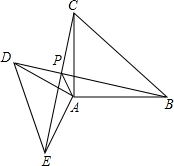 如图,在△ABC和△ADE中,∠CAB=∠DAE=90°,AB=AC=4,AD=AE=2,直线,CE交BD于点P,将△ADE绕点A旋转α角(0°<α<180°),在旋转过程中,S△PAB的最大值为2+2$\sqrt{3}$.
如图,在△ABC和△ADE中,∠CAB=∠DAE=90°,AB=AC=4,AD=AE=2,直线,CE交BD于点P,将△ADE绕点A旋转α角(0°<α<180°),在旋转过程中,S△PAB的最大值为2+2$\sqrt{3}$.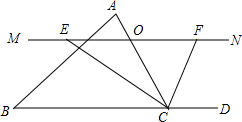 已知△ABC中,点O是边AC上的一个动点,过O做直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
已知△ABC中,点O是边AC上的一个动点,过O做直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.