题目内容
4. 如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,楼BC的高度大约为多少?(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)
如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,楼BC的高度大约为多少?(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)
分析 在Rt△ABD中,根据正切函数求得BD=AD•tan32°=31×0.6=18.6,在Rt△ACD中,求得CD=AD=31,再根据BC=BD+CD,代入数据计算即可.
解答 解:在Rt△ABD中,
∵AD=31,∠BAD=32°,
∴BD=AD•tan32°≈31×0.6=18.6,
在Rt△ACD中,
∵∠DAC=45°,
∴CD=AD=31,
∴BC=BD+CD=18.6+31≈50.
故楼BC的高度大约为50m.
点评 此题考查了解直角三角形的应用-仰角俯角问题.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若A(3,y1),B(5,y2),C(-2,y3)是抛物线y=-x2+4x+k上的三点,则y1、y2、y3的大小关系为( )
| A. | y2>y1>y3 | B. | y3>y2>y1 | C. | y1>y2>y3 | D. | y3>y1>y2 |
15.下列说法中正确的是( )
| A. | “作线段CD=AB”是一个命题 | |
| B. | 三角形的三条内角平分线交于一点 | |
| C. | 命题“若x=1,则x2=1”的逆命题是真命题 | |
| D. | 命题“两直线平行,内错角相等”的逆命题是假命题 |
19.正六边形的边心距为$\sqrt{3}$,这个正六边形的面积为( )
| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | 12 |
9. 如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
 如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )| A. | 一直减小 | B. | 一直不变 | C. | 先减小后增大 | D. | 先增大后减小 |
16.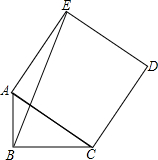 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,以斜边AC为边作正方形ACDE,连接BE,则BE的长是( )
如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,以斜边AC为边作正方形ACDE,连接BE,则BE的长是( )
 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,以斜边AC为边作正方形ACDE,连接BE,则BE的长是( )
如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,以斜边AC为边作正方形ACDE,连接BE,则BE的长是( )| A. | $2\sqrt{58}$ | B. | 14 | C. | $2\sqrt{65}$ | D. | $4\sqrt{13}$ |
13.下列二次根式中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{6}$ | C. | $\sqrt{8}$ | D. | $\sqrt{15}$ |