题目内容
19.正六边形的边心距为$\sqrt{3}$,这个正六边形的面积为( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | 12 |
分析 根据正六边形的特点,通过中心作边的垂线,连接半径,结合解直角三角形的有关知识解决.
解答 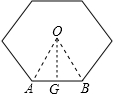 解:如图,连接OA、OB;过点O作OG⊥AB于点G.
解:如图,连接OA、OB;过点O作OG⊥AB于点G.
在Rt△AOG中,OG=$\sqrt{3}$,∠AOG=30°,
∵OG=OA•cos 30°,
∴OA=$\frac{OG}{cos30°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,
∴这个正六边形的面积=6S△OAB=6×$\frac{1}{2}$×2×$\sqrt{3}$=6$\sqrt{3}$.
故选C.
点评 此题主要考查正多边形和圆,根据题意画出图形,再根据正多边形的性质及锐角三角函数的定义解答即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.如图图形中,是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
11.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:
其中a为常数,且3≤a≤5
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
| 产品 | 每件售价(万元) | 每件成本(万元) | 每年其他费用(万元) | 每年最大产销量(件) |
| 甲 | 6 | a | 20 | 200 |
| 乙 | 20 | 10 | 40+0.05x2 | 80 |
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
9.若分式$\frac{x}{x-3}$有意义,则x满足的条件是( )
| A. | x≠0 | B. | x≠3 | C. | x≠-3 | D. | x≠±3 |
 如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,楼BC的高度大约为多少?(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)
如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,楼BC的高度大约为多少?(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)