题目内容
10.有四张扑克牌,分别为红桃3,红桃4,红桃5,黑桃6,背面朝上洗匀后放在桌面上,从中任取一张后记下数字和颜色,再背面朝上洗匀,然后再从中随机取一张,两次都为红桃,并且数字之和不小于8的概率为$\frac{1}{3}$.分析 先画树状图展示所有12种等可能的结果数,再找出两次都为红桃,并且数字之和不小于8的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有12种等可能的结果数,其中两次都为红桃,并且数字之和不小于8的结果数为4,
所以两次都为红桃,并且数字之和不小于8的概率=$\frac{4}{12}$=$\frac{1}{3}$.
故答案为$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
相关题目
1.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{14}$ | C. | $\sqrt{16}$ | D. | $\sqrt{18}$ |
18.若m2-m-1=0,则代数式m2-m+2013的值为( )
| A. | 2011 | B. | 2012 | C. | 2013 | D. | 2014 |
15.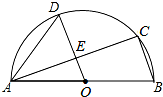 如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )
如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )
 如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )
如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )| A. | △AOD是等边三角形 | B. | $\widehat{AD}$=$\widehat{CD}$ | ||
| C. | ∠ACB=90° | D. | OE=$\frac{1}{2}$BC |
19.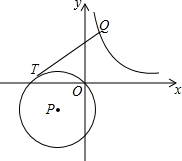 如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
 如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 4 |
 如图是一个正方体被截去一个正三棱锥得到的几何体,该几何体的俯视图为( )
如图是一个正方体被截去一个正三棱锥得到的几何体,该几何体的俯视图为( )



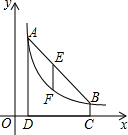 如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.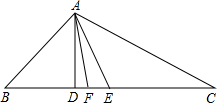 如图,完成下面几何语言的表达.
如图,完成下面几何语言的表达.