题目内容
叙述并证明三角形中位线定理.
考点:三角形中位线定理
专题:
分析:作出图形,然后写出已知、求证,延长EF到D,使FD=EF,利用“边角边”证明△AEF和△CDF全等,根据全等三角形对应边相等可得AE=CD,全等三角形对应角相等可得∠D=∠AEF,再求出CE=CD,根据内错角相等,两直线平行判断出AB∥CD,然后判断出四边形BCDE是平行四边形,根据平行四边形的性质可得DE∥BC,DE=BC.
解答: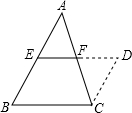 已知:△ABC中,点E、F分别是AB、AC的中点,
已知:△ABC中,点E、F分别是AB、AC的中点,
求证:EF∥BC且EF=
BC,
证明:如图,延长EF到D,使FD=EF,
∵点F是AC的中点,
∴AF=CF,
在△AEF和△CDF中,
,
∴△AEF≌△CDF(SAS),
∴AE=CD,∠D=∠AEF,
∴AB∥CD,
∵点E是AB的中点,
∴AE=BE,
∴BE=CD,
∴BE
CD,
∴四边形BCDE是平行四边形,
∴DE∥BC,DE=BC,
∴DE∥BC且DE=
BC.
 已知:△ABC中,点E、F分别是AB、AC的中点,
已知:△ABC中,点E、F分别是AB、AC的中点,求证:EF∥BC且EF=
| 1 |
| 2 |
证明:如图,延长EF到D,使FD=EF,
∵点F是AC的中点,
∴AF=CF,
在△AEF和△CDF中,
|
∴△AEF≌△CDF(SAS),
∴AE=CD,∠D=∠AEF,
∴AB∥CD,
∵点E是AB的中点,
∴AE=BE,
∴BE=CD,
∴BE
| ∥ |
. |
∴四边形BCDE是平行四边形,
∴DE∥BC,DE=BC,
∴DE∥BC且DE=
| 1 |
| 2 |
点评:本题考查了三角形的中位线定理的证明,关键在于作辅助线构造成全等三角形和平行四边形,文字叙述性命题的证明思路和方法需熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 无论k取任何实数,对于直线y=kx都会经过一个固定的点(0,0),我们就称直线y=kx恒过定点(0,0).
无论k取任何实数,对于直线y=kx都会经过一个固定的点(0,0),我们就称直线y=kx恒过定点(0,0).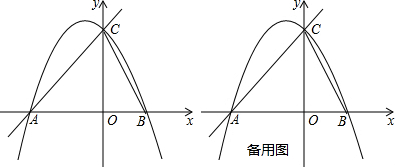
 如图,动直线y=kx(k>0)与抛物线y=ax2(a是常数,且a>0)相交与点O,A,以OA为边作矩形OABC.
如图,动直线y=kx(k>0)与抛物线y=ax2(a是常数,且a>0)相交与点O,A,以OA为边作矩形OABC.