题目内容
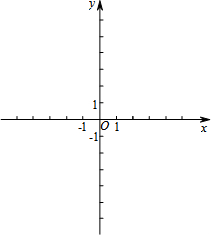 无论k取任何实数,对于直线y=kx都会经过一个固定的点(0,0),我们就称直线y=kx恒过定点(0,0).
无论k取任何实数,对于直线y=kx都会经过一个固定的点(0,0),我们就称直线y=kx恒过定点(0,0).(1)无论m取任何实数,抛物线y=mx2-(1+3m)x+2恒过定点A(x0,y0),直接写出定点A的坐标;
(2)已知△ABC的一个顶点是(1)中的定点A(x0>0),且∠B,∠C的角平分线分别是y轴和直线y=x,求边BC所在直线的表达式;
(3)求△ABC内切圆的半径.
考点:二次函数综合题
专题:
分析:(1)无论m为任何实数抛物线y=mx2-(1+3m)x+2恒过定点A(x0,y0),也就是说整理后m的系数等于0;
(2)由已知条件易求点A(x0>0)坐标,因为∠B,∠C的角平分线所在直线分别是y轴和直线y=x,所以点B、点C在点A关于y轴、直线y=x的对称点所确定的直线上.
作点A关于y轴的对称点D(-3,-1),作点A关于直线y=x的对称点E(-1,3),设直线BC的表达式为y=kx+b,把D,E点的坐标代入求出k和b的值即可;
(3)过点O作OF⊥BC于F,则OF即为△ABC内切圆的半径,设BC与x轴交点为点G,易知G(-
, 0),B(0,5),由三角形的面积为的值即可求出内切圆的半径.
(2)由已知条件易求点A(x0>0)坐标,因为∠B,∠C的角平分线所在直线分别是y轴和直线y=x,所以点B、点C在点A关于y轴、直线y=x的对称点所确定的直线上.
作点A关于y轴的对称点D(-3,-1),作点A关于直线y=x的对称点E(-1,3),设直线BC的表达式为y=kx+b,把D,E点的坐标代入求出k和b的值即可;
(3)过点O作OF⊥BC于F,则OF即为△ABC内切圆的半径,设BC与x轴交点为点G,易知G(-
| 5 |
| 2 |
解答: 解:(1)∵y=mx2-(1+3m)x+2=mx2-x-3mx+2,
解:(1)∵y=mx2-(1+3m)x+2=mx2-x-3mx+2,
=(x2-3x)m-x+2,
∴若要无论m取任何实数,抛物线y=mx2-(1+3m)x+2恒过定点A(x0,y0),则x2-3x=0,
∴x=0或3,
∴点A的坐标为(0,2),(3,-1).
(2)∵△ABC的一个顶点是(1)中的定点A(x0>0),
∴A(3,-1).
∵∠B,∠C的角平分线所在直线分别是y轴和直线y=x,
∴点B、点C在点A关于y轴、直线y=x的对称点所确定的直线上.
作点A关于y轴的对称点D(-3,-1),作点A关于直线y=x的对称点E(-1,3).
直线DE与y轴的交点即为点B,与直线y=x的交点即为点C.连接AB,AC.
设直线BC的表达式为y=kx+b.
则有
解之,得
所以,yBC=2x+5.
(3)∵∠B,∠C的角平分线所在直线分别是y轴和直线y=x,y轴和直线y=x的交点O即为△ABC内切圆的圆心.
过点O作OF⊥BC于F,则OF即为△ABC内切圆的半径.
设BC与x轴交点为点G,易知G(-
, 0),B(0,5).
∴BG=
.
∵S△BOG=
•OB•OG=
•GB•OF,
∴OF=
,即△ABC内切圆的半径为
.
 解:(1)∵y=mx2-(1+3m)x+2=mx2-x-3mx+2,
解:(1)∵y=mx2-(1+3m)x+2=mx2-x-3mx+2,=(x2-3x)m-x+2,
∴若要无论m取任何实数,抛物线y=mx2-(1+3m)x+2恒过定点A(x0,y0),则x2-3x=0,
∴x=0或3,
∴点A的坐标为(0,2),(3,-1).
(2)∵△ABC的一个顶点是(1)中的定点A(x0>0),
∴A(3,-1).
∵∠B,∠C的角平分线所在直线分别是y轴和直线y=x,
∴点B、点C在点A关于y轴、直线y=x的对称点所确定的直线上.
作点A关于y轴的对称点D(-3,-1),作点A关于直线y=x的对称点E(-1,3).
直线DE与y轴的交点即为点B,与直线y=x的交点即为点C.连接AB,AC.
设直线BC的表达式为y=kx+b.
则有
|
解之,得
|
所以,yBC=2x+5.
(3)∵∠B,∠C的角平分线所在直线分别是y轴和直线y=x,y轴和直线y=x的交点O即为△ABC内切圆的圆心.
过点O作OF⊥BC于F,则OF即为△ABC内切圆的半径.
设BC与x轴交点为点G,易知G(-
| 5 |
| 2 |
∴BG=
5
| ||
| 2 |
∵S△BOG=
| 1 |
| 2 |
| 1 |
| 2 |
∴OF=
| 5 |
| 5 |
点评:本题考查了用待定系数法求一次函数的解析式、三角形内切圆的性质、三角形的面积公式运用、轴对称的性质以及新定义的问题,题目的综合性较强,对学生的综合解题能力要求很高.

练习册系列答案
相关题目
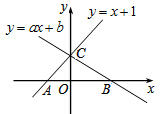 如图,直线y=ax+b(a≠0)与y=x+1交于y轴上的点C,与x轴交于点B(2,0).
如图,直线y=ax+b(a≠0)与y=x+1交于y轴上的点C,与x轴交于点B(2,0).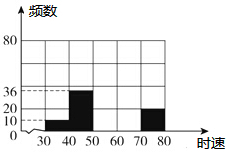 理,得到不完整的图表:
理,得到不完整的图表: