题目内容
 如图,动直线y=kx(k>0)与抛物线y=ax2(a是常数,且a>0)相交与点O,A,以OA为边作矩形OABC.
如图,动直线y=kx(k>0)与抛物线y=ax2(a是常数,且a>0)相交与点O,A,以OA为边作矩形OABC.(1)求点A的坐标(用含k、a的式子表示);
(2)设点B的坐标为(x,y),当点C恰好落在该抛物线上时,求y与x的函数关系式(用含a的式子表示);
(3)在(2)中求出的函数是否有最大(或最小)值?若有,求出其值,以及此时k的值,并判断此时四边形OABC的形状;若没有,说明理由.
考点:二次函数综合题
专题:
分析:(1)利用图象上点的坐标性质假设出A点坐标,进而代入解析式得出即可;
(2)首先利用△AOA′∽△OCC′.得出C点坐标,进而得出Rt△BDA≌Rt△CC′O(AAS),进而得出
-x=0-(-
),y-
=
,求出y与x的函数关系式;
(3)根据题意得出k的值,进而得出AO=CO,即可得出四边形OABC的形状.
(2)首先利用△AOA′∽△OCC′.得出C点坐标,进而得出Rt△BDA≌Rt△CC′O(AAS),进而得出
| k |
| a |
| 1 |
| ak |
| k2 |
| a |
| 1 |
| ak2 |
(3)根据题意得出k的值,进而得出AO=CO,即可得出四边形OABC的形状.
解答:解:(1)由题意可设点A的坐标为(xA,kxA),则kxA=ax
.
∴xA=
或 xA=0(舍),
∴点A的坐标为:(
,
);
(2)由题意可设点C的坐标为(xc,ax
),
作AA′⊥x轴,CC′⊥x轴,垂足分别为A′、C′.
则∠AA′O=∠CC′O=90°.
∵四边形OABC是矩形,
∴∠AOA′=180°-∠AOC-∠COC′=180°-90°-∠COC′=∠OCC′.
∴△AOA′∽△OCC′.
∴
=
即
=
•xc=-
.
∴点C坐标为(-
,
).
作 BB′⊥x轴,AD⊥BB′,垂足分别为B′、D.则∠BAD=90°-∠DAO,∠COC′=90°-∠AOB′.
∵∠ADB′=∠OB′D=90°,
∴DA∥OB′.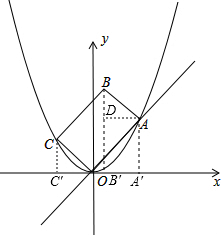
∴∠DAO=∠AOB′.
∴∠BAD=∠COC′.
又∵AB=OC,
在Rt△BDA和Rt△CC′O中,
,
∴Rt△BDA≌Rt△CC′O(AAS).
∴DA=C′O,BD=CC′,即
-x=0-(-
),y-
=
,
∴x=
(k-
),
y=
(k2+
)
=
[(k-
)2+2]
=
(a2x2+2)
=ax2+
;
(3)由a>0知,当x=0时,即k-
=0时,y有最小值,最小值为
,
则k-
=0,
解得,k1=1,k2=-1(舍).
故点A、C的坐标分别为:(
,
)、(-
,
).
则OA=OC=
.
又∵四边形OABC是矩形,
∴四边形OABC是正方形.
2 A |
∴xA=
| k |
| a |
∴点A的坐标为:(
| k |
| a |
| k2 |
| a |
(2)由题意可设点C的坐标为(xc,ax
2 c |
作AA′⊥x轴,CC′⊥x轴,垂足分别为A′、C′.
则∠AA′O=∠CC′O=90°.
∵四边形OABC是矩形,
∴∠AOA′=180°-∠AOC-∠COC′=180°-90°-∠COC′=∠OCC′.
∴△AOA′∽△OCC′.
∴
| AA′ |
| OA′ |
| OC′ |
| CC′ |
| ||
|
| -xc | ||
a
|
| 1 |
| ak |
∴点C坐标为(-
| 1 |
| ak |
| 1 |
| ak2 |
作 BB′⊥x轴,AD⊥BB′,垂足分别为B′、D.则∠BAD=90°-∠DAO,∠COC′=90°-∠AOB′.
∵∠ADB′=∠OB′D=90°,
∴DA∥OB′.

∴∠DAO=∠AOB′.
∴∠BAD=∠COC′.
又∵AB=OC,
在Rt△BDA和Rt△CC′O中,
|
∴Rt△BDA≌Rt△CC′O(AAS).
∴DA=C′O,BD=CC′,即
| k |
| a |
| 1 |
| ak |
| k2 |
| a |
| 1 |
| ak2 |
∴x=
| 1 |
| a |
| 1 |
| k |
y=
| 1 |
| a |
| 1 |
| k2 |
=
| 1 |
| a |
| 1 |
| k |
=
| 1 |
| a |
=ax2+
| 2 |
| a |
(3)由a>0知,当x=0时,即k-
| 1 |
| k |
| 2 |
| a |
则k-
| 1 |
| k |
解得,k1=1,k2=-1(舍).
故点A、C的坐标分别为:(
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
则OA=OC=
| ||
| a |
又∵四边形OABC是矩形,
∴四边形OABC是正方形.
点评:此题主要考查了函数图象上点的坐标性质和正方形的判定以及全等三角形和相似三角形的判定与性质等知识,得出A,C点坐标是解题关键.

练习册系列答案
相关题目
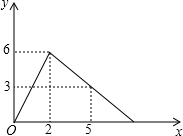 某医院研究所研发了一种新药,在临床试验时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(小时)的变化情况如图所示.?
某医院研究所研发了一种新药,在临床试验时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(小时)的变化情况如图所示.?