题目内容
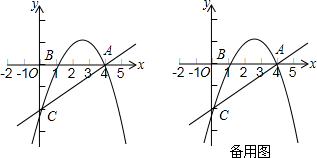
解下列不等式或不等式组,并把解集在数轴上表示出来.
(1)5(x-1)≤3(x+1);
(2)-2<1-
x<
;
(3)
.
(1)5(x-1)≤3(x+1);
(2)-2<1-
| 1 |
| 5 |
| 3 |
| 5 |
(3)
|
考点:解一元一次不等式组,在数轴上表示不等式的解集,解一元一次不等式
专题:
分析:(1)按照解不等式的步骤,利用不等式的基本性质:去括号,移项,系数化1,再在数轴上表示出来;
(2)(3)分别解两个不等式,求出其解集,在数轴上表示出来,找出公共部分,即求出了不等式组的解集.
(2)(3)分别解两个不等式,求出其解集,在数轴上表示出来,找出公共部分,即求出了不等式组的解集.
解答:解:(1)5(x-1)≤3(x+1)
5x-5≤3x+3
5x-3x≤3+5
2x≤8
x≤4

(2))-2<1-
x<
-3<-
x<-
解得:2<x<15

(3)(3)
解不等式①得:x<2
解不等式②得:x≥-1
所以不等式组的解集为:-1≤x<2.

5x-5≤3x+3
5x-3x≤3+5
2x≤8
x≤4

(2))-2<1-
| 1 |
| 5 |
| 3 |
| 5 |
-3<-
| 1 |
| 5 |
| 2 |
| 5 |
解得:2<x<15

(3)(3)
|
解不等式①得:x<2
解不等式②得:x≥-1
所以不等式组的解集为:-1≤x<2.

点评:此题考查解不等式或解不等式组,不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
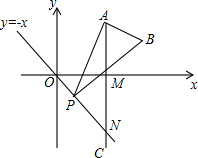 如图,已知点A是第一象限内横坐标为2
如图,已知点A是第一象限内横坐标为2| 3 |
| A、4 | ||
B、2
| ||
C、2
| ||
| D、2π |
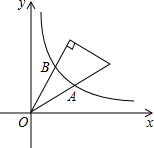 在平面直角坐标系中,一直角三角板如图放置,其30°角的两边与双曲线y=
在平面直角坐标系中,一直角三角板如图放置,其30°角的两边与双曲线y=| k |
| x |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
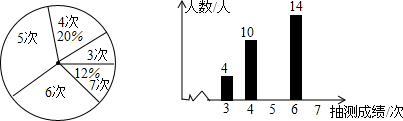
 有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行抽样调查,结果统计如下,其中扇形统计图中E组所在的扇形的圆心角为144°.
有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行抽样调查,结果统计如下,其中扇形统计图中E组所在的扇形的圆心角为144°.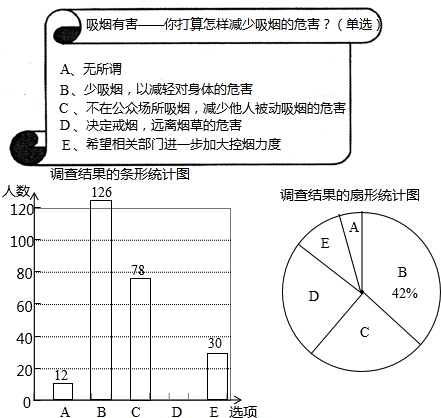
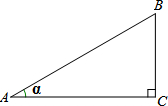 如图,定义:在Rt△ABC中,∠C=90°,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=
如图,定义:在Rt△ABC中,∠C=90°,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=