题目内容
19．
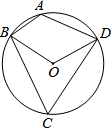如图，A，B，C，D为⊙O上四点，若∠BOD=110°，则∠A的度数是（ ）| A． | 110° | B． | 115° | C． | 120° | D． | 125° |
分析 由A，B，C，D为⊙O上四点，若∠BOD=110°，根据在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，即可求得∠C的度数，又由圆的内接四边形的性质定理，即可求得答案．
解答 解：∵A，B，C，D为⊙O上四点，∠BOD=110°，
∴∠C=$\frac{1}{2}$∠BOD=55°，
∴∠A=180°-∠C=125°．
故选D．
点评 此题考查了圆周角定理以及圆的内接四边形的性质．注意掌握圆的内接四边形的对角互补．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
9．下列二次根式中，能与$\sqrt{2}$合并的是（ ）
| A． | $\sqrt{20}$ | B． | $\sqrt{12}$ | C． | $\sqrt{8}$ | D． | $\sqrt{4}$ |
14．若分式$\frac{x-2}{x-1}$的值为0，则x的值为（ ）
| A． | 1或2 | B． | 2 | C． | 1 | D． | 0 |
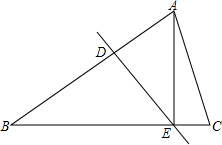如图所示，△ABC中，DE垂直平分AB，分别交AB、BC于点D、E
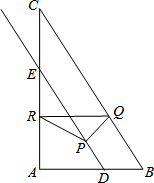如图，在Rt△ABC中，∠A=90°，AB=6，AC=8，D在AB上且AD=4，DE∥BC交AC于E，点P从点D出发沿射线DE运动，过点P作PQ⊥BC于Q，过点Q作QR∥AB交AC于R，当点Q与点C重合时，点P停止运动．设BQ=x，RQ=y．
3．等腰三角形的底边长10m，周长为36cm，则底角的正弦值为（ ）
| A． | $\frac{5}{18}$ | B． | $\frac{5}{16}$ | C． | $\frac{13}{15}$ | D． | $\frac{12}{13}$ |