题目内容
6.正六边形的边长为R,它的边心距为$\frac{\sqrt{3}}{2}$R.分析 连接OA、OB,作OC⊥AB于C,证出△AOB是等边三角形,得出AB=OA=R,∠AOC=30°,求出AC=$\frac{1}{2}$R,OC=$\sqrt{3}$AC=$\frac{\sqrt{3}}{2}$R即可.
解答 解:如图所示: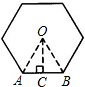 连接OA、OB,作OC⊥AB于C,
连接OA、OB,作OC⊥AB于C,
∵OA=OB,∠AOB=$\frac{360}{6}$=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=R,∠AOC=30°,
∴AC=$\frac{1}{2}$R,
∴OC=$\sqrt{3}$AC=$\frac{\sqrt{3}}{2}$R,
即半径为R的正六边形的边长为R,边心距为$\frac{\sqrt{3}}{2}$R;
故答案为:R,$\frac{\sqrt{3}}{2}$R.
点评 本题考查了正六边形的性质、等边三角形的判定与性质、勾股定理;熟练掌握正六边形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
1.下列各式中正确的是( )
| A. | -3(a-7)=-3a-21 | B. | 3a-(4a2+2)=3a-4a2+2 | ||
| C. | -[-(2a+3y)]=2a-3y | D. | -2x-y=-(2x+y) |
11.直角三角形的面积为4$\sqrt{3}$,两直角边的比是2:$\sqrt{3}$,则它的斜边长为( )
| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{7}$ |
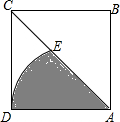 如图,正方形ABCD中,以A为圆心,AD为半径作弧交AC于E,若阴影部分的面积为2π,求AC的长.
如图,正方形ABCD中,以A为圆心,AD为半径作弧交AC于E,若阴影部分的面积为2π,求AC的长. 如图所示,将一个矩形沿图中的虚线折叠,用量角器测量一下其中的α,β,得α=β
如图所示,将一个矩形沿图中的虚线折叠,用量角器测量一下其中的α,β,得α=β