题目内容
17.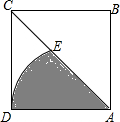 如图,正方形ABCD中,以A为圆心,AD为半径作弧交AC于E,若阴影部分的面积为2π,求AC的长.
如图,正方形ABCD中,以A为圆心,AD为半径作弧交AC于E,若阴影部分的面积为2π,求AC的长.
分析 设正方形ABCD的边长为x,根据正方形的性质与扇形的面积计算方法求得x,进一步利用勾股定理求得AC的长即可.
解答 解:∵四边形ABCD是正方形,
∴∠DAC=45°,AD=CD,
设正方形ABCD的边长为x,
则$\frac{45π{x}^{2}}{360}$=2π,
x2=16,
解得:x=4,
因此AC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
点评 此题考查三星的面积,正方形的性质,勾股定理,利用扇形的面积求得正方形的边长是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
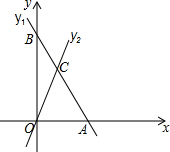 如图,在平面直角坐标系中,直线y1=kx+b与y2=3x交于点C(a,3),与x轴、y轴分别交于点A,B,点B的坐标为(0,5).
如图,在平面直角坐标系中,直线y1=kx+b与y2=3x交于点C(a,3),与x轴、y轴分别交于点A,B,点B的坐标为(0,5).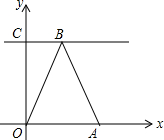 在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$,分别以OA,OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系;
在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$,分别以OA,OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系;