题目内容
14．
如图，在正方形ABCD中，点E，F在对角线BD上，若再添加一个条件，就可证出AE=CF．（1）你添加的条件是BE=DF．
（2）请你根据题目中的条件和你添加的条件证明AE=CF．
分析 （1）BE=DF（答案不唯一）；
（2）根据SAS即可证明△ABE≌△CDF可得AE=CF．
解答 解：（1）BE=DF（答案不唯一）．
（2）证明：∵四边形ABCD是正方形，
∴AB∥CD，AB=CD，
∴∠ABD=∠BDC，
又∵BE=DF（添加），
∴△ABE≌△CDF，
∴AE=CF．
点评 本题考查正方形的性质、全等三角形的判定和性质等知识，解题的关键是熟练掌握全等三角形的判定方法，属于中考常考题型．
练习册系列答案
相关题目
4．对于抛物线y=-$\frac{1}{2}$（x-1）2+3，下列说法正确的是（ ）
| A． | 开口向下，顶点坐标（1，3） | B． | 开口向上，顶点坐标（3，-1） | ||
| C． | 开口向下，顶点坐标（-1，3） | D． | 开口向上，顶点坐标（-3，1） |
9．一次函数y=-3x+5图象上有两点A（$\frac{2}{3}$，y1）、B（2，y2），则y1与y2的大小关系是（ ）
| A． | y1＞y2 | B． | y1＜y2 | C． | y1=y2 | D． | y1≤y2 |
19．
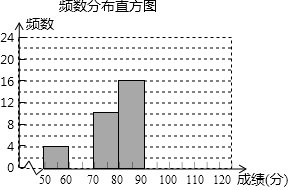2017年3月在北京市召开的第十二届全国人民代表大会第五次会议上，环境问题再次成为大家讨论的重点内容之一．2017年6月5日是世界环境日，为纪念第46个世界环境日，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛，为了了解本次竞赛成绩情况，从中抽取了50名学生的成绩进行统计分析，经分组整理后绘制成频数分布表和频数分布直方图．
频数分布表
（1）请你根据图表提供的信息，解答下列问题：a=8，b=12，c= 0.24；
（2）请补全频数分布直方图；
（3）若成绩在90分以上（含90分）为优秀，则该校成绩优秀的约为216人．
2017年3月在北京市召开的第十二届全国人民代表大会第五次会议上，环境问题再次成为大家讨论的重点内容之一．2017年6月5日是世界环境日，为纪念第46个世界环境日，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛，为了了解本次竞赛成绩情况，从中抽取了50名学生的成绩进行统计分析，经分组整理后绘制成频数分布表和频数分布直方图．频数分布表
| 分组/分 | 频数 | 频率 |
| 50～60 | 4 | 0.08 |
| 60～70 | a | 0.16 |
| 70～80 | 10 | 0.20 |
| 80～90 | 16 | 0.32 |
| 90～100 | b | c |
| 合计 | 50 | 1 |
（2）请补全频数分布直方图；
（3）若成绩在90分以上（含90分）为优秀，则该校成绩优秀的约为216人．