题目内容
9．一次函数y=-3x+5图象上有两点A（$\frac{2}{3}$，y1）、B（2，y2），则y1与y2的大小关系是（ ）| A． | y1＞y2 | B． | y1＜y2 | C． | y1=y2 | D． | y1≤y2 |
分析 利用一次函数的增减性判断即可．
解答 解：在一次函数y=-3x+5中，
∵k=-3＜0，
∴y随x的增大而减小，
∵$\frac{2}{3}$＜2，
∴y1＞y2，
故选A．
点评 本题主要考查一次函数的增减性，掌握一次函数的增减性是解题的关键，即在y=kx+b中，当k＞0时y随x的而增大，当k＜0时，y随x的增大而减小．
练习册系列答案
相关题目
如图所示，在四边形ABCD中，∠A=90°，AB=3，AD=4，BC=13，CD=12，求四边形ABCD的面积．
20．据统计2016年约有1770000人参加研究生考试，把1770000用科学记数法表示为（ ）
| A． | 177×104 | B． | 17.7×105 | C． | 1.77×106 | D． | 0.177×107 |
17．某学习小组的同学做摸球实验时，在一个暗箱里放了多个只有颜色不同的小球，将小球搅匀后任意摸出一个，记下颜色并放回暗箱，再次将球搅匀后任意摸出一个，不断重复．下表是实验过程中记录的数据：
请估计从暗箱中任意摸出一个球是白球的概率是0.6．
| 摸球的次数m | 300 | 400 | 500 | 800 | 1000 |
| 摸到白球的次数n | 186 | 242 | 296 | 483 | 599 |
| 摸到白球的频率$\frac{n}{m}$ | 0.620 | 0.605 | 0.592 | 0.604 | 0.599 |
4．
从共享单车，共享汽车等共享出行到共享雨伞等共享物品，各式各样的共享经济模式在各个领域迅速的普及，根据国家信息中心发布的中国分享经济发展报告2017显示，参与共享经济活动超6 亿人，比上一年增加约1亿人．
（1）为获得北京市市民参与共享经济活动信息，下列调查方式中比较合理的是C；
A．对某学校的全体同学进行问卷调查
B．对某小区的住户进行问卷调查
C．在全市里的不同区县，选取部分市民进行问卷调查
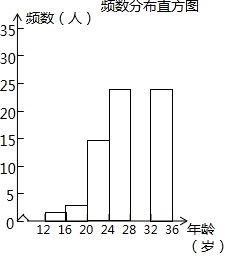
（2）调查小组随机调查了延庆区市民骑共享单车情况，某社区年龄在12～36岁的人有1000人，从中随机抽取了100人，统计了他们骑共享单车的人数，并绘制了如下不完整的统计图表．如图所示．
骑共享单车的人数统计表
根据以上信息解答下列问题：
①统计表中的a=0.15；b=30；
②补全频数分布直方图；
③试估计这个社区年龄在20岁到32岁（含20岁，不含32岁）骑共享单车的人有多少人？
从共享单车，共享汽车等共享出行到共享雨伞等共享物品，各式各样的共享经济模式在各个领域迅速的普及，根据国家信息中心发布的中国分享经济发展报告2017显示，参与共享经济活动超6 亿人，比上一年增加约1亿人．（1）为获得北京市市民参与共享经济活动信息，下列调查方式中比较合理的是C；
A．对某学校的全体同学进行问卷调查
B．对某小区的住户进行问卷调查
C．在全市里的不同区县，选取部分市民进行问卷调查
（2）调查小组随机调查了延庆区市民骑共享单车情况，某社区年龄在12～36岁的人有1000人，从中随机抽取了100人，统计了他们骑共享单车的人数，并绘制了如下不完整的统计图表．如图所示．
骑共享单车的人数统计表
| 年龄段（岁） | 频数 | 频率 |
| 12≤x＜16 | 2 | 0.02 |
| 16≤x＜20 | 3 | 0.03 |
| 20≤x＜24 | 15 | a |
| 24≤x＜28 | 25 | 0.25 |
| 28≤x＜32 | b | 0.30 |
| 32≤x＜36 | 25 | 0.25 |
①统计表中的a=0.15；b=30；
②补全频数分布直方图；
③试估计这个社区年龄在20岁到32岁（含20岁，不含32岁）骑共享单车的人有多少人？
如图，在正方形ABCD中，点E，F在对角线BD上，若再添加一个条件，就可证出AE=CF．
1．将公式$\frac{1}{R}$=$\frac{1}{{R}_{1}}$$+\frac{1}{{R}_{2}}$（R，R1，R2均不为零，且R≠R2）变形成求R1的式子，正确的是（ ）
| A． | R1=$\frac{R{R}_{2}}{{R}_{2}-R}$ | B． | R1=$\frac{R{R}_{2}}{{R}_{2}+R}$ | C． | R1=$\frac{R{R}_{1}+R{R}_{2}}{{R}_{2}}$ | D． | R1=$\frac{R{R}_{2}}{R-{R}_{2}}$ |
已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=AH，连接BG并延长交DE于F．