题目内容
2．设函数y=$\frac{1}{x}$与y=2x+1的图象的交点坐标为（a，b），求$\frac{1}{a}$-$\frac{2}{b}$的值．分析 由函数y=$\frac{1}{x}$与y=2x+1的图象的交点为（a，b）知ab=1、b=2a+1，代入到$\frac{1}{a}$-$\frac{2}{b}$=$\frac{b}{ab}$-$\frac{2a}{ab}$=$\frac{b-2a}{ab}$可得答案．
解答 解：∵函数y=$\frac{1}{x}$与y=2x+1的图象的交点为（a，b），
∴ab=1，b=2a+1，
∴$\frac{1}{a}$-$\frac{2}{b}$=$\frac{b}{ab}$-$\frac{2a}{ab}$=$\frac{b-2a}{ab}$=$\frac{1}{1}$=1．
点评 本题主要考查反比例函数与一次函数的交点问题，掌握反比例函数与一次函数图象的交点坐标满足每个解析式是解题的关键．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
12．某果农种了50棵苹果树，收获时，他把苹果树的产量做了一下统计，得到下表：
（1）苹果产量的众数是35千克；中位数是35千克；平均数是35千克；
（2）市场上苹果的销售价为8元/千克，化肥、农药、人工费等共投入资金1000元，则今年该果农纯收入多少元？
| 质量（千克） | 33 | 34 | 35 | 36 | 38 |
| 数量（棵） | 10 | 5 | 20 | 10 | 5 |
（2）市场上苹果的销售价为8元/千克，化肥、农药、人工费等共投入资金1000元，则今年该果农纯收入多少元？
10．下列图形中，不是中心对称图形但是轴对称图形的是（ ）
| A． |  等腰三角形 | B． |  平行四边形 | C． |  矩形 | D． |  菱形 |
17．某学习小组的同学做摸球实验时，在一个暗箱里放了多个只有颜色不同的小球，将小球搅匀后任意摸出一个，记下颜色并放回暗箱，再次将球搅匀后任意摸出一个，不断重复．下表是实验过程中记录的数据：
请估计从暗箱中任意摸出一个球是白球的概率是0.6．
| 摸球的次数m | 300 | 400 | 500 | 800 | 1000 |
| 摸到白球的次数n | 186 | 242 | 296 | 483 | 599 |
| 摸到白球的频率$\frac{n}{m}$ | 0.620 | 0.605 | 0.592 | 0.604 | 0.599 |
对于点P（x，y），规定x+y=a，那么就把a叫点P的亲和数．例如：若P（2，3），则2+3=5，那么5叫P的亲和数．
如图，在正方形ABCD中，点E，F在对角线BD上，若再添加一个条件，就可证出AE=CF．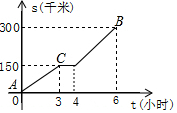
杨师傅开车从A地出发去300千米远的B地游玩，其行驶路程s与时间t之间的关系如图所示，出发一段时间后，汽车发生故障，需停车检修，修好后又继续行驶．根据题意回答下列问题：