题目内容
17. 如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD:∠BOC=5:1,则∠COE的度数为( )
如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD:∠BOC=5:1,则∠COE的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
分析 由已知两角之比,设出∠BOC=x,∠AOD=5x,再由两个直角,利用周角为360°列出关于x的方程,求出方程的解得到x的值,确定出∠BOC的度数,进而求出∠BOD度数,根据OE为角平分线,求出∠BOE度数,根据∠BOE-∠BOC求出∠COE度数即可.
解答 解:由∠AOD:∠BOC=5:1,设∠BOC=x,∠AOD=5x,
∵∠AOB=∠COD=90°,
∴5x+x=360°-90°-90°,
解得:x=30°,
∴∠BOC=30°,
∴∠BOD=∠BOC+∠COD=120°,
∵OE为∠BOD平分线,
∴∠BOE=∠DOE=60°,
则∠COE=∠BOE-∠BOC=30°,
故选A
点评 此题考查了角平分线定义,以及周角定义,熟练掌握角平分线定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( ) 共青团县委准备在艺术节期间举办学生绘画展览,为美化画面,在长30cm、宽20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图所示),若设彩纸的宽度为xcm,则列方程整理成一般形式为x2+25x-150=0.
共青团县委准备在艺术节期间举办学生绘画展览,为美化画面,在长30cm、宽20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图所示),若设彩纸的宽度为xcm,则列方程整理成一般形式为x2+25x-150=0. 在?ABCD中,∠A比∠B大30°,求∠C的度数.
在?ABCD中,∠A比∠B大30°,求∠C的度数.
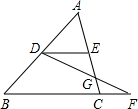 如图,在△ABC中,D、E分别是AB和AC的中点,F是BC延长线上一点,DF平分CE于点G,CF=2,则BC=4.
如图,在△ABC中,D、E分别是AB和AC的中点,F是BC延长线上一点,DF平分CE于点G,CF=2,则BC=4.