题目内容
7.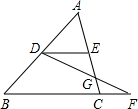 如图,在△ABC中,D、E分别是AB和AC的中点,F是BC延长线上一点,DF平分CE于点G,CF=2,则BC=4.
如图,在△ABC中,D、E分别是AB和AC的中点,F是BC延长线上一点,DF平分CE于点G,CF=2,则BC=4.
分析 根据三角形的中位线平行于第三边并且等于第三边的一半可得BC=2DE,DE∥BC,再根据两直线平行,内错角相等可得∠DEG=∠FCG,然后利用“角边角”证明△DEG和△FCG全等,根据全等三角形对应边相等可得DE=CF,然后求解即可.
解答 解:∵D、E分别是AB和AC的中点,
∴DE=$\frac{1}{2}$BC,DE∥BC,
∴∠DEG=∠FCG,
∵DF平分CE于点G,
∴EG=CG,
∵在△DEG和△FCG中,
$\left\{\begin{array}{l}{∠DEG=∠FCG}\\{EG=CG}\\{∠DGE=∠FGC}\end{array}\right.$,
∴△DEG≌△FCG(ASA),
∴DE=CF,
∵CF=2,
∴DE=2,
∴BC=2DE=2×2=4.
故答案是:4.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半的性质,全等三角形的判定与性质,是基础题,熟练掌握定理并判定出三角形全等是解题的关键.

练习册系列答案
相关题目
17. 如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD:∠BOC=5:1,则∠COE的度数为( )
如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD:∠BOC=5:1,则∠COE的度数为( )
 如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD:∠BOC=5:1,则∠COE的度数为( )
如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD:∠BOC=5:1,则∠COE的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
18.下列四组数据不能作为直角三角形的三边长的是( )
| A. | 0.3、0.4、0.5 | B. | 1、$\sqrt{2}$、$\sqrt{3}$ | C. | 3、5、6 | D. | 5、12、13 |
15.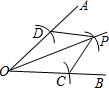 如图,用尺规作图画角平分线:以O为圆心,任意长为半径画弧交OA,OB于点C,D,再分别以C,D为圆心,以大于$\frac{1}{2}CD$长为半径画弧,两弧交于点P,由此得△POC≌△POD依据是( )
如图,用尺规作图画角平分线:以O为圆心,任意长为半径画弧交OA,OB于点C,D,再分别以C,D为圆心,以大于$\frac{1}{2}CD$长为半径画弧,两弧交于点P,由此得△POC≌△POD依据是( )
 如图,用尺规作图画角平分线:以O为圆心,任意长为半径画弧交OA,OB于点C,D,再分别以C,D为圆心,以大于$\frac{1}{2}CD$长为半径画弧,两弧交于点P,由此得△POC≌△POD依据是( )
如图,用尺规作图画角平分线:以O为圆心,任意长为半径画弧交OA,OB于点C,D,再分别以C,D为圆心,以大于$\frac{1}{2}CD$长为半径画弧,两弧交于点P,由此得△POC≌△POD依据是( )| A. | AAS | B. | SAS | C. | SSS | D. | ASA |
2.若关于x的一元二次方程x2-2x+k=0有两个不相等的实数根,则k的取值范围是( )
| A. | k<1 | B. | k≤1 | C. | k>-1 | D. | k>1 |
17.小丽同学准备用自己节省的零花钱购买一台学生平板电脑,她已存有750元,并计划从本月起每月节省30元,直到她至少存有1080元,设x个月后小丽至少有1080元,则可列计算月数的不等式为( )
| A. | 30x+750>1080 | B. | 30x-750≥1080 | C. | 30x-750≤1080 | D. | 30x+750≥1080 |