题目内容
 如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y=x+1的图象为直线l2,与x轴交于点C;两直线l1,l2相交于点B.
如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y=x+1的图象为直线l2,与x轴交于点C;两直线l1,l2相交于点B.(1)求k、b的值;
(2)求点B的坐标;
(3)求△ABC的面积.
考点:两条直线相交或平行问题
专题:
分析:(1)将A点和D点的坐标代入到一次函数的一般形式,求得k、b的值即可;
(2)两函数联立组成方程组求得方程组的解后即可求得点B的坐标;
(3)首先求得点C的坐标,然后利用S△ABC=S△ACD-S△BCD求解即可.
(2)两函数联立组成方程组求得方程组的解后即可求得点B的坐标;
(3)首先求得点C的坐标,然后利用S△ABC=S△ACD-S△BCD求解即可.
解答:解:(1)把A(0,4)和D(4,0)代入y=kx+b得:
,
解得
;
(2)由(1)得y=-x+4,联立
,
解得
,
所以B(
,
);
(3)由y=x+1,当y=0时,x+1=0,解得x=-1,
所以点C(-1,0)
所以S△ABC=S△ACD-S△BCD=
×5×4-
×5×2=5;
|
解得
|
(2)由(1)得y=-x+4,联立
|
解得
|
所以B(
| 3 |
| 2 |
| 5 |
| 2 |
(3)由y=x+1,当y=0时,x+1=0,解得x=-1,

所以点C(-1,0)
所以S△ABC=S△ACD-S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了两条直线平行或相交的问题,求两条直线的交点坐标时通常联立后组成方程组求解.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、近似数2.4×105精确到十分位 |
| B、近似数5.04×105与近似数50400一样 |
| C、将数60340保留两个有效数字,得6.0×104 |
| D、用四舍五入法得到的近似数8.1750精确到0.001 |
代数式a2、-xyz、
、-x、
、0、a2+b2、-0.2中单项式的个数是( )
| ab2 |
| 4 |
| b |
| a |
| A、4 | B、5 | C、6 | D、7 |
 如图,大正方形的边长为a,小正方形的边长为2,求阴影部分的面积.
如图,大正方形的边长为a,小正方形的边长为2,求阴影部分的面积.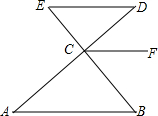 如图,已知∠B=∠E,∠A=∠FCD,试问ED与CF平行吗?为什么?
如图,已知∠B=∠E,∠A=∠FCD,试问ED与CF平行吗?为什么? 如图,要在燃气管道l上修建一个泵站C,分别向A、B两住宅小区供气,泵站修在管道的什么地方,可使所用的输气管线最短?请你在管道l上画出这个位置C,要求尺规作图,不写作法,保留作图痕迹.
如图,要在燃气管道l上修建一个泵站C,分别向A、B两住宅小区供气,泵站修在管道的什么地方,可使所用的输气管线最短?请你在管道l上画出这个位置C,要求尺规作图,不写作法,保留作图痕迹. 两个数相差2,设其中较大的一个数为x,它们的积为y.
两个数相差2,设其中较大的一个数为x,它们的积为y. 填空并解答问题:已知:如图,线段AB=14cm,点C为线段AB上一点,点D、E分别为线段AB、AC的中点,ED=1cm,求线段AC的长.
填空并解答问题:已知:如图,线段AB=14cm,点C为线段AB上一点,点D、E分别为线段AB、AC的中点,ED=1cm,求线段AC的长.