题目内容
 两个数相差2,设其中较大的一个数为x,它们的积为y.
两个数相差2,设其中较大的一个数为x,它们的积为y.(1)写出y关于x的函数表达式;
(2)画出相应的函数图象;
(3)请描述y随x的变化而变化的情况.
考点:二次函数的应用
专题:
分析:(1)根据题意表示出较小数,表示出两数之积y与x的关系式即可;
(2)求出顶点、与x轴的交点及对称轴,进而画出图象;
(3)根据图象找出y随x的变化而变化的情况即可.
(2)求出顶点、与x轴的交点及对称轴,进而画出图象;
(3)根据图象找出y随x的变化而变化的情况即可.
解答:解:(1)∵两数相差2,其中较大的一个数为x,
∴另一个数为(x-2),
∴y=x(x-2)=(x-1)2-1;
(2)由函数表达式可知图象的顶点坐标为(1,-1),与x轴的坐标为(0,0)、(2,0),对称轴为x=1,
由此可作函数图象,如图所示:

(3)有图可知,当x<1时,y随x的增大而减小;当x>1时,y随x的增大而增大.
∴另一个数为(x-2),
∴y=x(x-2)=(x-1)2-1;
(2)由函数表达式可知图象的顶点坐标为(1,-1),与x轴的坐标为(0,0)、(2,0),对称轴为x=1,
由此可作函数图象,如图所示:

(3)有图可知,当x<1时,y随x的增大而减小;当x>1时,y随x的增大而增大.
点评:此题考查了二次函数的应用,以及函数的三种表达式,弄清题意是解本题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
有4条线段,长分别是:2,3,4,5,从中任取3条,可以组成三角形的情况有( )
| A、0种 | B、1种 | C、2种 | D、3种 |
 如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y=x+1的图象为直线l2,与x轴交于点C;两直线l1,l2相交于点B.
如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y=x+1的图象为直线l2,与x轴交于点C;两直线l1,l2相交于点B. 如图,ABCD是400米的环形跑道,现在把跑道分成相等的4段,即两条直道和两条弯道长度都相同.甲、乙二人沿着环形跑道ABCD练习跑步(匀速),甲从A点出发,乙从B点出发,甲比乙每秒多跑1米.
如图,ABCD是400米的环形跑道,现在把跑道分成相等的4段,即两条直道和两条弯道长度都相同.甲、乙二人沿着环形跑道ABCD练习跑步(匀速),甲从A点出发,乙从B点出发,甲比乙每秒多跑1米. 如图,已知数轴上有A、B、C三个点,它们表示的数分别是-24,-10,10.
如图,已知数轴上有A、B、C三个点,它们表示的数分别是-24,-10,10.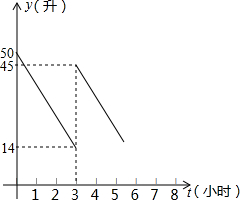 汽车出发前油箱有油50L,行驶若干小时后,在加油站加油若干升.图象表示的是从出发后,油箱中剩余油量y(L)与行驶时间t(h)之间的关系.
汽车出发前油箱有油50L,行驶若干小时后,在加油站加油若干升.图象表示的是从出发后,油箱中剩余油量y(L)与行驶时间t(h)之间的关系.