题目内容
17.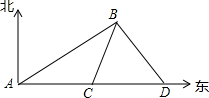 如图,某船在海上航行,在A处观测到灯塔B在北偏东60°方向上,该船以每小时15海里的速度向东航行到达C处,观测到灯塔B在北偏东30°方向上,继续向东航行到D处,观测到灯塔B在北偏西30°方向上,当该船到达D处时恰与灯塔B相距60海里.
如图,某船在海上航行,在A处观测到灯塔B在北偏东60°方向上,该船以每小时15海里的速度向东航行到达C处,观测到灯塔B在北偏东30°方向上,继续向东航行到D处,观测到灯塔B在北偏西30°方向上,当该船到达D处时恰与灯塔B相距60海里.(1)判断△BCD的形状;
(2)求该船从A处航行至D处所用的时间;
(3)若该船从A处向东航行6小时到达E处,观测灯塔B,灯塔B在什么方向上?
分析 (1)根据题意可得∠BCD=∠BDC=60°,即可知△BCD是等边三角形;
(2)由(1)可求得BC,CD的长,然后易证得△ABC是等腰三角形,继而求得AD的长,则可求得该船从A处航行至D处所用的时间;
(3)首先过点B作BH⊥CD于点H,可求得AH的距离,继而求得到点H的时间,求得E点与H点重合,可得灯塔B在正北方向上.
解答 解:(1)根据题意得:∠BCD=90°-30°=60°,∠BDC=90°-30°=60°,
∴∠BCD=∠BDC=60°,
∴BC=BD,
∴△BCD是等边三角形;
(2)∵△BCD是等边三角形,
∴CD=BD=BC=60海里,
∵∠BAC=90°-60°=30°,
∴∠ABC=∠BCD-∠BAC=30°,
∴∠BAC=∠ABC,
∴AC=BC=60海里,
∴AD=AC+CD=120海里,
∴该船从A处航行至D处所用的时间为:120÷15=8(小时);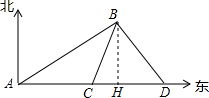 (3)过点B作BH⊥CD于点H,
(3)过点B作BH⊥CD于点H,
∵△BCD是等边三角形,
∴CH=$\frac{1}{2}$CD=30海里,
∴AH=AC+CH=90海里,
∴该船从A处向东航行到达H处所用时间为:90÷15=6(小时),
∴E点与H点重合,
∴灯塔B在正北方向上.
点评 此题考查了方向角问题.注意准确构造直角三角形是解此题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
6.已知x=1是方程(k-1)x2+x-2=0的一个根,则方程的另一个根是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
 =_______________________.
=_______________________.
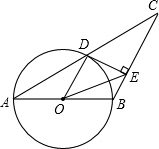 如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,并过点D作⊙O的切线交BC于点E,若CD=10,CE=8.
如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,并过点D作⊙O的切线交BC于点E,若CD=10,CE=8.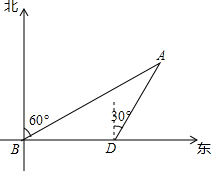 如图,海中有一小岛A,它的周围10海里内有暗礁,渔船由西向东航行.在B点测得小岛A在北偏东60°方向,再航行12海里到达D点,这时测得小岛A在北偏东30°方向.如果渔船不改变航向,继续向东航行,有没有触礁的危险?
如图,海中有一小岛A,它的周围10海里内有暗礁,渔船由西向东航行.在B点测得小岛A在北偏东60°方向,再航行12海里到达D点,这时测得小岛A在北偏东30°方向.如果渔船不改变航向,继续向东航行,有没有触礁的危险?