题目内容
6.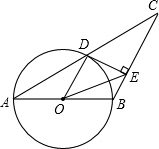 如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,并过点D作⊙O的切线交BC于点E,若CD=10,CE=8.
如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,并过点D作⊙O的切线交BC于点E,若CD=10,CE=8.求:(1)DE的长;
(2)⊙O的半径.
分析 (1)连结BD,如图,利用圆周角定理得到∠ADB=90°,再根据等腰三角形的性质得AD=CD,则OD=$\frac{1}{2}$BC,OD∥BC,接着利用切线的性质得到OD⊥DE,所以DE⊥BC,然后利用勾股定理计算DE的长;
(2)证明Rt△CDE∽Rt△CBD,利用相似比求出BC,从而得到OD的长.
解答 解:(1)连结BD,如图,
∵AB为直径,
∴∠ADB=90°,
∴BD⊥AC,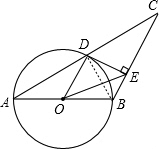
而BA=BC,
∴AD=CD,
而OA=OB,
∴OD为△ABC的中位线,
∴OD=$\frac{1}{2}$BC,OD∥BC,
∵DE为切线,
∴OD⊥DE,
∴DE⊥BC,
在Rt△CDE中,DE=$\sqrt{C{D}^{2}-C{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6;
(2)∵∠DCE=∠BCD,
∴Rt△CDE∽Rt△CBD,
∴CD:CB=CE:CD,即10:CB=8:10,解得CB=$\frac{25}{2}$,
∴OD=$\frac{1}{2}$BC=$\frac{25}{4}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.解决(1)小题的关键是证明DE⊥BC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.(6x-2y)2•(-xy)-2=( )
| A. | 36x-6 | B. | 36x-3 | C. | -12x-2y4 | D. | -36x-3y |
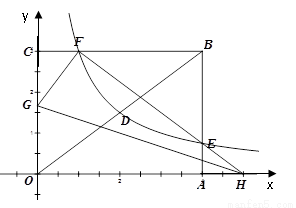
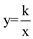 (k≠0)在第一象限内的图象经过点D、E,且
(k≠0)在第一象限内的图象经过点D、E,且
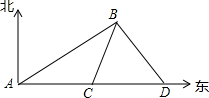 如图,某船在海上航行,在A处观测到灯塔B在北偏东60°方向上,该船以每小时15海里的速度向东航行到达C处,观测到灯塔B在北偏东30°方向上,继续向东航行到D处,观测到灯塔B在北偏西30°方向上,当该船到达D处时恰与灯塔B相距60海里.
如图,某船在海上航行,在A处观测到灯塔B在北偏东60°方向上,该船以每小时15海里的速度向东航行到达C处,观测到灯塔B在北偏东30°方向上,继续向东航行到D处,观测到灯塔B在北偏西30°方向上,当该船到达D处时恰与灯塔B相距60海里.
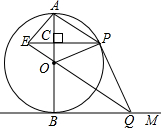 如图,AB是⊙0的直径,BM切⊙0于点B,点P是⊙0上的一个动点(不经过A、B两点),过点0作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ.
如图,AB是⊙0的直径,BM切⊙0于点B,点P是⊙0上的一个动点(不经过A、B两点),过点0作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ.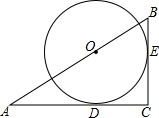 如图,△ABC中,以AB上一点O为圆心的⊙O分别与AC、BC相切于D、E,若AC=4,BC=3,求⊙O的半径.
如图,△ABC中,以AB上一点O为圆心的⊙O分别与AC、BC相切于D、E,若AC=4,BC=3,求⊙O的半径. 完成下面证明
完成下面证明