题目内容
2.在直角坐标系中,如果以坐标原点O为圆心的圆与直线y=-$\sqrt{3}$x+2$\sqrt{3}$相切于点C,求:(1)⊙O的半径.
(2)切点C的坐标.
分析 (1)如图,利用一次函数图象上点的坐标特征求出A点和B点坐标,再利用锐角三角函数求出∠BAO的度数,接着关键切线的性质得到OC⊥AB,然后在Rt△OCA中利用正弦定义可求出OC的长;
(2)作CD⊥OA于D,如图,在Rt△OCD中利用含30度的直角三角形三边的关系求出CD和OD的长,从而可得到C点坐标.
解答 解:(1)如图,直线y=-$\sqrt{3}$x+2$\sqrt{3}$交x轴于A点,交y轴于B点,连结OC,
当y=0时,-$\sqrt{3}$x+2$\sqrt{3}$=0,解得x=2,则A(2,0);
当x=0时,y=-$\sqrt{3}$x+2$\sqrt{3}$=2$\sqrt{3}$,则B(0,2$\sqrt{3}$),
在Rt△OAB中,∵OA=2,OB=2$\sqrt{3}$,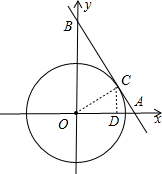
∴tan∠BAO=$\frac{OB}{OA}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴∠BAO=60°,
∵AB为切线,
∴OC⊥AB,
在Rt△OCA中,∵sin∠CAO=$\frac{OC}{OA}$,
∴OC=2sin60°=$\sqrt{3}$,
即⊙O的半径为$\sqrt{3}$;
(2)作CD⊥OA于D,如图,
在Rt△OCD中,∵∠COD=30°,
∴CD=$\frac{1}{2}$OC=1,OD=$\sqrt{3}$CD=$\sqrt{3}$,
∴C点坐标为($\sqrt{3}$,1).
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.解决(1)小题的关键是确定∠OAB的度数,解决(2)小题的关键是求C点到x轴和y轴的距离.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
13.如图,∠1和∠2是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
11.(6x-2y)2•(-xy)-2=( )
| A. | 36x-6 | B. | 36x-3 | C. | -12x-2y4 | D. | -36x-3y |
 B.
B.  C.
C.  D.
D. 
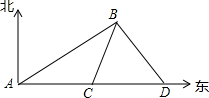 如图,某船在海上航行,在A处观测到灯塔B在北偏东60°方向上,该船以每小时15海里的速度向东航行到达C处,观测到灯塔B在北偏东30°方向上,继续向东航行到D处,观测到灯塔B在北偏西30°方向上,当该船到达D处时恰与灯塔B相距60海里.
如图,某船在海上航行,在A处观测到灯塔B在北偏东60°方向上,该船以每小时15海里的速度向东航行到达C处,观测到灯塔B在北偏东30°方向上,继续向东航行到D处,观测到灯塔B在北偏西30°方向上,当该船到达D处时恰与灯塔B相距60海里.
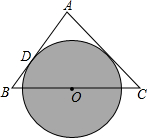 如图,在△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,求证:AC是⊙O的切线.(提示:证明切线的基本思路:不知共点,作垂直,证半径)
如图,在△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,求证:AC是⊙O的切线.(提示:证明切线的基本思路:不知共点,作垂直,证半径)