题目内容
5．反比例函数y=$\frac{{k}^{2}-2k-3}{x}$在每一个象限内y随x的增大而增大，则k的取值范围是-1＜k＜3．分析 根据反比例函数的性质得出关于k的不等式，求出k的取值范围即可．
解答 解：∵反比例函数y=$\frac{{k}^{2}-2k-3}{x}$在每一个象限内y随x的增大而增大，
∴k2-2k-3＜0，解得-1＜k＜3．
故答案为：-1＜k＜3．
点评 本题考查的是反比例函数的性质，熟知反比例函数的增减性是解答此题的关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
如图，AB=AC=5，BC=8，∠DAC=90°，则BD的长为$\frac{7}{4}$，AD=$\frac{15}{4}$．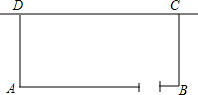
现有长28米的网，围成一个一面靠墙的矩形鸡舍：已知墙长14米，AB边可开一个或两个1米宽的门．
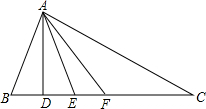如图，