题目内容
15. 如图,AB=AC=5,BC=8,∠DAC=90°,则BD的长为$\frac{7}{4}$,AD=$\frac{15}{4}$.
如图,AB=AC=5,BC=8,∠DAC=90°,则BD的长为$\frac{7}{4}$,AD=$\frac{15}{4}$.
分析 作AE⊥BC于E.根据等腰三角形三线合一的性质得出BE=EC=$\frac{1}{2}$BC=4,利用勾股定理求出AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=3.再设DE=x,在Rt△DAC与Rt△DAE中,根据勾股定理得到AD2=DC2-AC2=DE2+AE2,即(x+4)2-52=x2+32,解方程求出x的值,进而求解即可.
解答  解:如图,作AE⊥BC于E.
解:如图,作AE⊥BC于E.
∵AB=AC,AE⊥BC于E,BC=8,
∴BE=EC=$\frac{1}{2}$BC=4,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3.
设DE=x,则BD=4-x,DC=x+4.
在Rt△DAC中,∵∠DAC=90°,
∴AD2=DC2-AC2,
在Rt△DAE中,∵∠DEA=90°,
∴AD2=DE2+AE2,
∴DC2-AC2=DE2+AE2,
即(x+4)2-52=x2+32,
解得x=$\frac{9}{4}$,
∴BD=4-$\frac{9}{4}$=$\frac{7}{4}$,
AD2=($\frac{9}{4}$)2+32=$\frac{225}{16}$,AD=$\frac{15}{4}$.
故答案为$\frac{7}{4}$,$\frac{15}{4}$.
点评 本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.也考查了勾股定理,根据勾股定理得出DC2-AC2=DE2+AE2是解题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
7.某学校新建阶梯教室,第一排有25个座位,后面每排都比前一排多一个座位,若第n排有m个座位,教室共有p个座位.
(1)写出m与n,p与n之间的函数式;
(2)若教室座位共有15排,座位总数将达到多少个?
(1)写出m与n,p与n之间的函数式;
(2)若教室座位共有15排,座位总数将达到多少个?
4. 如图,AD⊥BC于D,DE是△ADC的中线,则以AD为高的三角形有( )
如图,AD⊥BC于D,DE是△ADC的中线,则以AD为高的三角形有( )
 如图,AD⊥BC于D,DE是△ADC的中线,则以AD为高的三角形有( )
如图,AD⊥BC于D,DE是△ADC的中线,则以AD为高的三角形有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
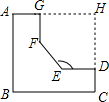 一个零件的形状如图所示,按规定∠A=∠B=∠C=∠D=∠G=90°,∠E=140°,质检工人测得∠F=140°,就断定这个零件不合格,这是为什么?
一个零件的形状如图所示,按规定∠A=∠B=∠C=∠D=∠G=90°,∠E=140°,质检工人测得∠F=140°,就断定这个零件不合格,这是为什么?