题目内容
12. 如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236.
分析 首先过点B作BD⊥AC于点D,进而利用BD=AB•sin∠BAD,BC=$\frac{BC}{sin∠BCD}$求出即可
解答  解:解:过点B作BD⊥AC于点D,
解:解:过点B作BD⊥AC于点D,
由题意可知:∠BAC=45°,∠ABC=90°+15°=105°,
则∠ACB=180°-∠BAC-∠ABC=30°,
在Rt△ABD中,BD=AB•sin∠BAD=20×$\frac{\sqrt{2}}{2}$=10$\sqrt{2}$,
在Rt△BCD中,BC=$\frac{BD}{sin∠BCD}$=20$\sqrt{2}$.
答:此时船C与船B的距离是20$\sqrt{2}$海里.
点评 此题主要考查了方向角问题,根据题意得出BD的长是解题关键.

练习册系列答案
相关题目
20.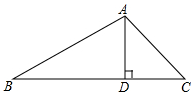 如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
 如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )| A. | 10 | B. | 10$\sqrt{2}$ | C. | 10$\sqrt{3}$ | D. | 15 |
17.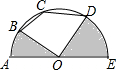 如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )
如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )
 如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )
如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )| A. | 2π | B. | 4π | C. | 8π | D. | 16π |

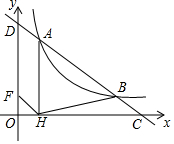 如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=6,则k的值为3.
如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=6,则k的值为3.