题目内容
2.请大家阅读下面两段材料,并解答问题:
材料1:我们知道在数轴上表示3和1的两点之间的距离为2(如图1),而|3-1|=2,所以在数轴上表示3和1的两点之间的距离为|3-1|.
再如在数轴上表示4和-2的两点之间的距离为6(如图2)而|4-(-2)|=6,所以数轴上表示数4和-2的两点之间的距离为|4-(-2)|.
根据上述规律,我们可以得出结论:在数轴上表示数a和数b两点之间的距离等于|a-b|(如图3)
试一试,求在数轴上表示的数5$\frac{2}{3}$与-4$\frac{1}{4}$的两点之间的距离为9$\frac{11}{12}$.
材料2:如图4所示大正方形的边长为a,小正方形的边长为b,则阴影部分的面积可表示为:a2-b2.
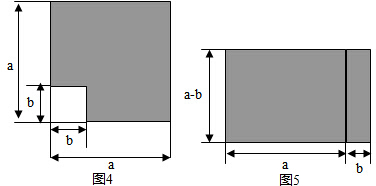
将图4中的图形重新拼接成图5,则阴影部分的面积可表示为(a+b)(a-b),并且可以得到等式:
a2-b2=(a+b)(a-b),请用此公式计算:${(999\frac{8}{9})}^{2}$-${(999\frac{1}{9})}^{2}$=1554$\frac{7}{9}$.
阅读后思考:
上述两段材料中,主要体现了数学中数与形相结合的数学思想.请运用此数学思想,求1+$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{128}$的值.
分析 材料1:根据数轴上两点间的距离=两个数之差的绝对值,算出即可;
材料2:利用平方差公式把题目展开成平方差公式的形式,然后根据有理数的加法法则计算,并且这样计算比较简便;
阅读后思考:利用图形分别表示出$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,$\frac{1}{16}$,…,结合阴影部分表示出结果即可.
解答 解:材料1:在数轴上表示的数5$\frac{2}{3}$与-4$\frac{1}{4}$的两点之间的距离为:|5$\frac{2}{3}$-(-4$\frac{1}{4}$)|=9$\frac{11}{12}$;
材料2:${(999\frac{8}{9})}^{2}$-${(999\frac{1}{9})}^{2}$=(999$\frac{8}{9}$+999$\frac{1}{9}$)(999$\frac{8}{9}$-999$\frac{1}{9}$)=1554$\frac{7}{9}$;
阅读后思考:如图,
由图形可知:
$\frac{1}{2}$+$\frac{1}{4}$=$\frac{3}{4}$,
$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$=$\frac{7}{8}$,
$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$=$\frac{15}{16}$,
所以1+$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{128}$=1+$\frac{127}{128}$=1$\frac{127}{128}$.
故答案为9$\frac{11}{12}$;1554$\frac{7}{9}$.
点评 本题考查了平方差公式的几何表示,关键是理解题意,才能根据题目的公式进行计算,此题还考查了数形结合的思想.

 一次函数y=ax+b的图象如图所示,则化简|a-b|+|b+1|得( )
一次函数y=ax+b的图象如图所示,则化简|a-b|+|b+1|得( )| A. | 2b-a+1 | B. | 1-a | C. | a-1-2b | D. | a+1 |
| A. | x-2=3(18-x) | B. | x+2=3(18-x) | C. | x+2=3(18+x) | D. | x-2=3(18+x) |
 如图,△ABC是等边三角形,P是△ABC的角平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC、BD于点F、Q,若BF=2,则PE的长为$\sqrt{3}$.
如图,△ABC是等边三角形,P是△ABC的角平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC、BD于点F、Q,若BF=2,则PE的长为$\sqrt{3}$.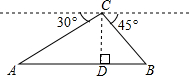 马航MH370失联以来,中国政府高度重视,每天军方派遣多架飞机、多艘军舰进行海上联合搜寻,某一天,从飞机C处测得A、B两艘军舰的俯角分别为30°、45°,此时飞机C处的高度CD为400米,点A,D,B在同一直线上,则A、B两艘军舰的距离是400($\sqrt{3}$+1)米.(结果保留根号)
马航MH370失联以来,中国政府高度重视,每天军方派遣多架飞机、多艘军舰进行海上联合搜寻,某一天,从飞机C处测得A、B两艘军舰的俯角分别为30°、45°,此时飞机C处的高度CD为400米,点A,D,B在同一直线上,则A、B两艘军舰的距离是400($\sqrt{3}$+1)米.(结果保留根号)