题目内容

17．（1）-22-$\sqrt{{（-7）}^{2}}$+$\root{3}{\frac{27}{8}}$       
（2）若$\sqrt{a-1}$+（b-2）2+|a+c|=0，求a+b-c的平方根．

分析 （1）原式利用乘方的意义，二次根式性质，以及立方根定义计算即可得到结果；
（2）根据已知等式，利用非负数的性质求出a，b，c的值，即可确定出a+b-c的平方根．

解答 解：（1）原式=-4-7+$\frac{3}{2}$=-9$\frac{1}{2}$；
（2）∵$\sqrt{a-1}$+（b-2）2+|a+c|=0，
∴a-1=0，b-2=0，a+c=0，
解得：a=1，b=2，c=-1，
则a+b-c=1+2+1=4，即4的平方根为±2．

点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
7．如图，AB∥CD，∠C=42°，∠E=58°，则∠B的度数为（　　）
A．120°B．128°C．80°D．100°
8．将一正方体纸盒沿下图所示的线剪开，则展开图的形状为（　　）
A．B．C．D．
5．通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，试猜想EF、BE、DF之间的数量关系．

（1）思路梳理
把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，由∠ADG=∠B=90°，得∠FDG=180°，即点F、D、G共线，易证△AFG≌△AFE，故EF、BE、DF之间的数量关系为BE+FD=EF．
（2）类比引申
如图2，点E、F分别在正方形ABCD的边CB、DC的延长线上，∠EAF=45°．连接EF，试猜想EF、BE、DF之间的数量关系，并给出证明．
（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．若BD=1，EC=2，则DE的长为$\sqrt{5}$．
12．用科学记数法表示-0.004023=-4.023×10-3．
2．请大家阅读下面两段材料，并解答问题：

材料1：我们知道在数轴上表示3和1的两点之间的距离为2（如图1），而|3-1|=2，所以在数轴上表示3和1的两点之间的距离为|3-1|．
再如在数轴上表示4和-2的两点之间的距离为6（如图2）而|4-（-2）|=6，所以数轴上表示数4和-2的两点之间的距离为|4-（-2）|．
根据上述规律，我们可以得出结论：在数轴上表示数a和数b两点之间的距离等于|a-b|（如图3）
试一试，求在数轴上表示的数5$\frac{2}{3}$与-4$\frac{1}{4}$的两点之间的距离为9$\frac{11}{12}$．
材料2：如图4所示大正方形的边长为a，小正方形的边长为b，则阴影部分的面积可表示为：a2-b2．

将图4中的图形重新拼接成图5，则阴影部分的面积可表示为（a+b）（a-b），并且可以得到等式：
a2-b2=（a+b）（a-b），请用此公式计算：${（999\frac{8}{9}）}^{2}$-${（999\frac{1}{9}）}^{2}$=1554$\frac{7}{9}$．
阅读后思考：
上述两段材料中，主要体现了数学中数与形相结合的数学思想．请运用此数学思想，求1+$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{128}$的值．
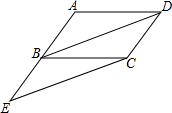9．已知：如图，在?ABCD中，延长AB到E，使得BE=AB，连接BD、CE．
（1）求证：BD∥CE；
（2）请在所给的图中，用直尺和圆规作点F（不同于图中已给的任何点），使对F、B、E、C为顶点的四边形是平行四边形（只作一个，保留痕迹，不写作法）．
6．（1）4ab2-4a2b-b3；
（2）（2a-b）2+8ab．
7．已知$\frac{x}{y}$=$\frac{3}{4}$，求$\frac{x+y}{2x-y}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网