题目内容
10.如图3×3数表各行,各列及两条对角线之和彼此相等,设为S,求证:| a | b | c |
| d | e | f |
| g | h | i |
(2)2(a+c+g+i)=b+d+f+h+4e.
分析 (1)根据题意得出S=a+e+i,S=b+e+h,S=c+e+g,相加即可得出答案;
(2)根据题意得出(a+b+c)+(a+d+g)+(g+h+i)+(i+f+c)=4S,再变形即可得出答案.
解答 解:(1)由题意得:S=a+e+i,S=b+e+h,S=c+e+g,
则3=(a+b+c)+3e+(i+h+g),
3S=S+3e+S,
S=3e;
(2)∵(a+b+c)+(a+d+g)+(g+h+i)+(i+f+c)=4S,
∴2(a+c+g+i)=4S-(b+d+h+f)
∵(b+e+h)+(d+e+f)=2S,
∴2S=b+h+d+f+2e
∴2(a+c+g+i)=2(b+d+f+h+2e)-(b+d+h+f)
∴2(a+c+g+i)=b+d+f+h+4e.
点评 本题考查了有理数的加法的应用,能根据有理数的加法法则进行变形是解此题的关键,难度不是很大.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 如图所示,CB=CE,∠BCE=∠ACD,请只补充一个条件,使得△ABC≌△DEC,并说明理由.
如图所示,CB=CE,∠BCE=∠ACD,请只补充一个条件,使得△ABC≌△DEC,并说明理由.

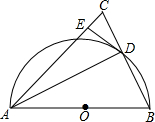 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.