在Rt△ABC中.∠C=90°.sin∠A=$\frac{3}{5}$.则tan∠B的值为$\frac{4}{3}$．题目和参考答案——青夏教育精英家教网—

题目内容

7．在Rt△ABC中，∠C=90°，sin∠A=$\frac{3}{5}$，则tan∠B的值为$\frac{4}{3}$．

分析作出图形，设BC=3k，AB=5k，利用勾股定理列式求出AC，再根据锐角的余切即可得解．

解答解：如图，

∵sin∠A=$\frac{3}{5}$，
∴设BC=3k，AB=5k，
由勾股定理得，AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4k，
∴tan∠B=$\frac{AC}{BC}=\frac{4k}{3k}=\frac{4}{3}$．
故答案为：$\frac{4}{3}$．

点评本题考查了互余两角三角函数的关系，利用“设k法”表示出三角形的三边求解更加简便．

练习册系列答案

相关题目

17．

如图，Rt△ABC中，∠ACB=90°，AC=BC=2，在以AB的中点O为坐标原点，AB所在直线为x轴建立的平面直角线坐标系中，将△ABC绕点B顺时针旋转，使点A旋转至y轴正半轴上的A′处，则图中阴影部分面积为$\frac{2π}{3}$．

18．

如图所示，CB=CE，∠BCE=∠ACD，请只补充一个条件，使得△ABC≌△DEC，并说明理由．

15．为反映某地区一周内每天最高气温的变化情况，应制作折线（填“扇形”或“条形”或“折线”）统计图．

2．请大家阅读下面两段材料，并解答问题：

材料1：我们知道在数轴上表示3和1的两点之间的距离为2（如图1），而|3-1|=2，所以在数轴上表示3和1的两点之间的距离为|3-1|．
再如在数轴上表示4和-2的两点之间的距离为6（如图2）而|4-（-2）|=6，所以数轴上表示数4和-2的两点之间的距离为|4-（-2）|．
根据上述规律，我们可以得出结论：在数轴上表示数a和数b两点之间的距离等于|a-b|（如图3）
试一试，求在数轴上表示的数5$\frac{2}{3}$与-4$\frac{1}{4}$的两点之间的距离为9$\frac{11}{12}$．
材料2：如图4所示大正方形的边长为a，小正方形的边长为b，则阴影部分的面积可表示为：a²-b²．

将图4中的图形重新拼接成图5，则阴影部分的面积可表示为（a+b）（a-b），并且可以得到等式：
a²-b²=（a+b）（a-b），请用此公式计算：${（999\frac{8}{9}）}^{2}$-${（999\frac{1}{9}）}^{2}$=1554$\frac{7}{9}$．
阅读后思考：
上述两段材料中，主要体现了数学中数与形相结合的数学思想．请运用此数学思想，求1+$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{128}$的值．

12．（1）用简便方法计算：2008²-4016×2001+2001²
（2）先化简，再求值：（$\frac{a}{b}$-$\frac{b}{a}$）÷$\frac{{a}^{2}+ab}{{a}^{2}b}$，其中a=-$\frac{1}{3}$，b=-$\frac{1}{2}$．

19．

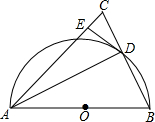如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD．过点D作DE⊥AC，垂足为点E．
（1）求证：DE是⊙O的切线；
（2）求证：BD²=AB•CE．

16．

二次函数y=-x²+ax-b的图象如图所示，则一次函数y=ax+b的图象不经过（　　）

17．计算：$\sqrt{{4}^{2}}$-$\sqrt{（-2）^{2}}$+（-3$\sqrt{5}$）²-（-$\sqrt{7}$）²．

试题分类