题目内容
2.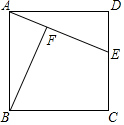 如图,已知E是正方形ABCD的边CD上一点,BF⊥AE于F.
如图,已知E是正方形ABCD的边CD上一点,BF⊥AE于F.(1)求证:△ABF∽△EAD;
(2)当AD=2$\sqrt{10}$,$\frac{DE}{EC}$=$\frac{1}{2}$时,求AF的长.
分析 (1)根据两角对应相等的两个三角形相似即可证明.
(2)首先求出DE、AE,由△ABF∽△EAD,得$\frac{AF}{DE}$=$\frac{AB}{AE}$,由此即可解决问题.
解答 (1)证明:∵正方形ABCD中,AB∥CD,
∴∠BAF=∠AED,
∵BF⊥AE,
∴∠AFB=90°,
∴∠AFB=∠D=90°,
∴△ABF∽△EAD.
(2)解:∵四边形ABCD是正方形,
∴AD=CD=AB=2$\sqrt{10}$
∵$\frac{DE}{EC}$=$\frac{1}{2}$,
∴DE=$\frac{1}{3}$CD=$\frac{2}{3}$$\sqrt{10}$,
在Rt△ADE中,AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{(2\sqrt{10})^{2}+(\frac{2}{3}\sqrt{10})^{2}}$=$\frac{20}{3}$,
∵△ABF∽△EAD,
∴$\frac{AF}{DE}$=$\frac{AB}{AE}$,
∴$\frac{AF}{\frac{2}{3}\sqrt{10}}$=$\frac{2\sqrt{10}}{\frac{20}{3}}$,
∴AF=2.
点评 本题考查正方形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列各组数据不能作为直角三角形的三边长的是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 13,16,18 |
17.菱形的两条对角线的长分别是6和8,则这个菱形的周长是( )
| A. | 24 | B. | 20 | C. | 10 | D. | 5 |
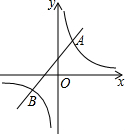 如图,已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
如图,已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2). 如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,求∠ABD的度数.
如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,求∠ABD的度数.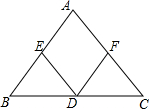 如图,D、E、F分别是BC、AB、AC的点,DF∥AB,DE∥AC,∠FDE=70°,求∠A的度数.
如图,D、E、F分别是BC、AB、AC的点,DF∥AB,DE∥AC,∠FDE=70°,求∠A的度数. 已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{{{({a+1})}^2}}$+$\sqrt{{{({b-1})}^2}}$-|a-b|.
已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{{{({a+1})}^2}}$+$\sqrt{{{({b-1})}^2}}$-|a-b|.