题目内容
13.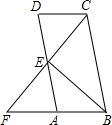 如图,在?ABCD中,E为AD的中点,CE交BA的延长线于F.
如图,在?ABCD中,E为AD的中点,CE交BA的延长线于F.(1)试证明:点A为FB的中点;
(2)若AD=2AB,∠BCD=110°,求∠ABE的度数.
分析 (1)由平行四边形的性质得出AB=CD,由AAS证明△DEC≌△AEF,得出CD=AF即可;
(2)由(1)可知FB=2AB,由BC=2AB,得出△FBC为等腰三角形,求出∠FBC的度数,由EF=EC,根据等腰三角形“三线合一”得出BE平分∠CBF,即可得出结果.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠DCE=∠F,∠FBC+∠BCD=180°,
∵E为AD的中点,
∴DE=AE.
在△DEC和△AEF中,$\left\{\begin{array}{l}{∠DCE=∠F}\\{∠DEC=∠AEF}\\{DE=AE}\end{array}\right.$,
∴△DEC≌△AEF(AAS).
∴DC=AF.
∴AB=AF,
即点A为FB的中点;
(2)解:由(1)可知BF=2AB,EF=EC,
∵∠BCD=110°,
∴∠FBC=180°-110°=70°,
∵BC=2AB,
∴BF=BC,
∴BE平分∠CBF,
∴∠ABE=$\frac{1}{2}$∠FBC=$\frac{1}{2}$×70°=35°.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.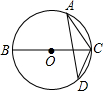 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是( )
 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
8.已知x=$\frac{1}{1+\sqrt{2}}$,y=$\frac{1}{1-\sqrt{2}}$,则$\sqrt{3{x}^{2}-5xy+3{y}^{2}}$的值是$\sqrt{23}$.
2.下列事件中,属于必然事件的是( )
| A. | 明天会下雨 | |
| B. | 小强期末数学考试会得100分 | |
| C. | 深圳冬天会下雪 | |
| D. | 从一个只装有10个红球的袋子里任意摸出一个刚好是红球 |